多头物理信息神经网络（Multi-Head Physics-Informed Neural Networks）

论文L-HYDRA: Multi-Head Physics-Informed Neural Networks（《L-HYDRA: 多头物理信息神经网络》）旨在将多头神经网络（Multi-Head Neural Networks, MH-NNs）引入物理信息神经网络（Physics-Informed Neural Networks, PINNs）框架中，以增强其在科学机器学习（SciML）中的多任务学习（Multi-Task Learning, MTL）、生成建模和少样本学习等方面的表现。文章从理论和应用的角度对MH-PINNs进行了详细描述，并通过一系列基准测试证明其有效性。

论文作者为Zongren Zou和George Em Karniadakis，来自Brown University（布朗大学）。

以下为论文概要内容：

一、研究背景

科学机器学习中，许多科学问题在本质上存在着相似性或者共享的物理规律，因此跨任务学习（learning across tasks）逐渐成为研究的重点。通过在多个相似任务之间共享知识，可以大幅提高模型的泛化能力和学习效率。例如，逼近随机过程、解偏微分方程（Partial Differential Equations, PDEs）、以及处理参数化的PDEs等场景中，不同任务之间常常存在内在的联系。因此，如何有效地构建能够处理多任务的神经网络框架是本研究的重点。

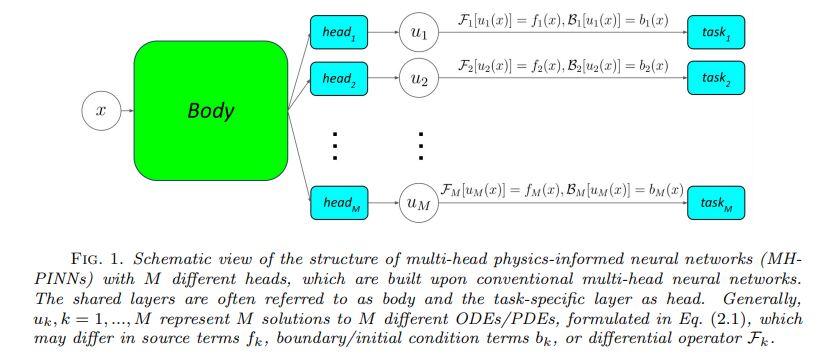
多头神经网络（MH-NNs）是一种硬参数共享的多任务学习方法，它通过一个共享的主体部分（body）和多个任务特定的头部（head）实现多个任务的同时学习。在本研究中，作者将这种思想引入物理信息神经网络（PINNs）中，形成了多头物理信息神经网络（MH-PINNs），以此来处理多任务学习、生成建模、以及少样本学习问题。

二、方法论：MH-PINNs的设计与实现

1. 多头神经网络与物理信息神经网络的结合

MH-PINNs基于传统的MH-NNs结构进行扩展，包含一个主体部分和多个头部。主体部分由多个非线性层构成，而每个头部为一个线性输出层，分别对应不同的任务。具体而言，MH-PINNs的主体部分用于提取共享的基础表示，这些表示可以看作是多个任务的公共特征，而每个头部则负责不同的任务。这样一来，多个任务通过共享主体部分的表示得到联系，同时每个头部保持对特定任务的独立性。

论文中提到，MH-PINNs通过以下两种方式实现了对多任务的连接：

共享基础函数：通过一个共享的主体部分（即网络的隐藏层）来连接多个任务，每个任务使用独立的头部来完成特定任务的学习。
共享分布信息：通过利用正态流（Normalizing Flows, NFs）对头部进行密度估计，从而形成一个共享的分布模型。这种分布信息用于生成建模以及不确定性量化等。

2. MH-PINNs的学习过程

MH-PINNs的学习过程可以分为两个阶段：

第一阶段：通过MH-NNs对多个任务进行联合训练，利用多任务之间的共享信息提高整体的学习效率。在这个过程中，模型中的主体部分会学习多个任务的公共特征，而每个头部则独立处理各自的任务。
第二阶段：通过正态流（NFs）对每个任务头部的输出进行密度估计，从而实现生成建模。正态流是一种生成模型，它既可以用于密度估计，也可以用于样本的生成。因此，作者选择正态流而非其他常见的生成模型（如生成对抗网络GANs、变分自编码器VAEs等），以便在生成建模和密度估计中都具有更高的灵活性。

3. MH-PINNs的应用

MH-PINNs的应用场景涵盖了多任务学习、生成建模、以及少样本学习等。具体而言，MH-PINNs可以用于以下目的：

逼近随机过程：通过物理信息生成方法，MH-PINNs可以有效地逼近具有随机特性的物理过程。
少样本学习（Few-shot Learning）：MH-PINNs可以为下游任务（如元学习和迁移学习）提供有用的先验知识，从而在数据稀缺的情况下提升学习效果。
不确定性量化（Uncertainty Quantification, UQ）：通过对头部进行密度估计，MH-PINNs可以实现对模型输出的生成建模与不确定性量化。

三、实验验证与结果分析

论文通过五个基准实验对MH-PINNs的有效性进行了验证，涵盖了多任务学习、回归问题、生成建模和少样本学习等多个领域。

1. 实验设置

函数逼近：研究者首先在一个函数逼近问题上验证了MH-PINNs的多任务学习和生成建模能力。函数形式为随机过程，通过MH-NNs对多个不同的函数进行联合训练，最终实现对目标函数的逼近和生成。
非线性常微分方程系统：研究者在一个非线性常微分方程系统上进行了测试，通过MH-PINNs学习外力项的随机过程，并比较了不同生成模型（如RealNVP、MAF和IAF）的效果。
一维非线性反应扩散方程：对一维的非线性反应扩散方程进行测试，验证了MH-PINNs在生成建模和不确定性量化中的有效性。
二维Allen-Cahn方程和二维Helmholtz方程：通过这些较为复杂的物理场景，验证了MH-PINNs在逼近复杂多维随机过程中的表现，以及在不确定性量化和少样本学习中的优越性。

2. 实验结果

在多任务学习（MTL）中，MH-PINNs通过共享的主体部分实现了多个任务的联合学习，在函数逼近和方程求解中展现了很好的泛化性能。
在生成建模方面，实验结果表明MH-PINNs结合正态流（NFs）能够有效地逼近目标分布，并生成符合随机过程特性的样本。
在少样本学习中，MH-PINNs利用从多任务学习中获得的共享基础函数和生成建模中的先验知识，大大提高了在数据不足情况下的学习效果，并通过贝叶斯推断实现了对不确定性的定量描述。

四、对比分析

论文还对MH-PINNs与其他相关方法进行了对比分析，特别是与传统的物理信息神经网络（PINNs）、生成对抗网络（GANs）和物理信息生成对抗网络（PI-GANs）等进行了详细比较。结果表明：

与传统的PINNs相比，MH-PINNs通过多任务学习和共享基础函数，提高了对相似任务的学习效率和预测准确性。
与PI-GANs相比，MH-PINNs由于采用了两阶段的学习方法，极大地提高了生成建模的灵活性和训练的稳定性，尤其是在物理信息学习和生成建模之间进行了解耦，使得训练过程更加简洁、易于控制。

五、应用前景与挑战

MH-PINNs为科学机器学习中的多任务学习、生成建模和少样本学习提供了一种有效的工具，其应用前景广泛，尤其在以下几个方面：

科学计算中的多任务求解：MH-PINNs能够有效解决多个相关联的偏微分方程问题，大大减少训练时间并提高求解效率。
生成建模与物理推断：通过生成模型，MH-PINNs能够对复杂的随机过程进行建模，这对于物理问题中的参数估计、不确定性分析等具有重要意义。
数据稀缺情况下的模型应用：在数据获取困难的场景下（例如一些实验物理学或气候模拟中），MH-PINNs通过少样本学习可以显著提升模型的准确性和稳定性。

不过，MH-PINNs在实践中仍然面临一些挑战，例如：

基础函数的表示能力：当不同任务之间具有显著差异时，强行共享基础函数可能会影响个别任务的表现，这对基础函数的设计提出了更高要求。
损失函数的平衡问题：在多任务学习中，不同任务的损失项如何权衡对模型的整体性能有较大影响，如何设置合理的权重来平衡不同任务的损失仍然是一个值得研究的问题。
任务间的协同学习与负迁移问题：在多任务学习中，如何充分利用任务间的相似性而避免负迁移（即任务之间相互干扰而降低学习效果）是一个重要的问题，后续需要在理论和实验中对此进行更深入的研究。

六、总结

总的来说，这篇论文通过引入多头神经网络的思想，提出了一种新的多头物理信息神经网络（MH-PINNs），并通过正态流实现了生成建模和不确定性量化。在科学机器学习领域，MH-PINNs展现了强大的多任务学习和少样本学习能力，能够有效解决偏微分方程、多任务回归等复杂问题，同时对模型的生成能力和不确定性分析提供了新的工具和思路。