内积（Inner Product）应用的一个简单形象实例：用户向量与物品向量的内积反映“喜好程度”

内积（Inner Product）是线性代数中一个基本而核心的概念，是衡量两个向量之间相似程度或“对齐程度”的数学工具。在不同的语境下，内积也被称为点积（Dot Product）、数量积（Scalar Product），在信息检索、机器学习中常用来衡量两个向量的相似性。以下是对内积的详细解释：

一、几何直观解释

设有两个向量：

• a=(a_1,a₂,…,a_n)
• b=(b₁,b₂,…,b_n)

它们的内积定义为：

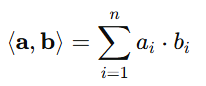
这是最常用的 欧几里得空间 中的内积形式，也称为标准内积。

几何意义：

内积可以表达为：

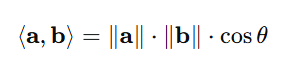
其中：

• ∥a∥ 和 ∥b∥ 是向量的欧几里得范数（长度）
• θ 是两个向量之间的夹角

当两个向量方向完全一致（同向），夹角为 0°，cosθ=1，内积最大；
当它们正交（垂直），cosθ=0，内积为0；
当它们方向相反（反向），cosθ=-1，内积为负数。

二、在机器学习与信息检索中的应用

在信息检索（IR）和推荐系统中，内积常用来衡量两个向量之间的“相关性”或“相似度”：

• 文本检索中，query 向量和 document 向量的内积越大，表示内容越相关；
• 推荐系统中，用户向量与物品向量的内积越大，表示用户可能越喜欢该物品；
• 神经网络中，attention机制（如Transformer）就大量使用了内积（Q·K^T）。

例如，如果我们用 BERT 模型将句子编码为向量，那么比较两个句子的语义是否相近，可以通过它们向量的内积来判断。

优点：

计算简单，易于在大规模向量库中使用；

与向量范数结合后，可转化为余弦相似度（cosine similarity）。

三、具体数值例子：说明用户向量与物品向量的内积如何反映“喜好程度”

🧠 场景设定：推荐系统中的内积相似度

假设我们有一个非常简化的推荐系统，用户和商品都被表示为长度为 3 的向量：

• 用户的偏好向量（User Embedding）表示他对属性【甜度、辛辣、热度】的偏好程度；
• 商品的特征向量（Item Embedding）表示该商品在这三种属性上的实际表现。

👤 用户向量

假设一个用户偏好如下：u=[0.9, 0.1, 0.5]

含义解释：

• 喜欢甜的程度是 0.9
• 喜欢辣的程度是 0.1
• 喜欢热食的程度是 0.5

🍜 商品A向量（辣椒热汤）：

i_A=[0.2, 0.9, 0.8]

含义解释：

• 微甜
• 非常辣
• 很热

🍰 商品B向量（冰镇甜点）：

i_B=[0.95, 0.05, 0.1]

含义解释：

• 很甜
• 不辣
• 冷的

🔢 计算用户与每个商品的内积

我们用向量内积来计算“匹配度”：

对商品A：

⟨u,i_A⟩=(0.9⋅0.2)+(0.1⋅0.9)+(0.5⋅0.8)=0.18+0.09+0.40=0.67

对商品B：

⟨u,i_B⟩=(0.9⋅0.95)+(0.1⋅0.05)+(0.5⋅0.1)=0.855+0.005+0.05=0.91

✅ 结果分析

• 商品B（冰镇甜点）匹配度 = 0.91
• 商品A（辣椒热汤）匹配度 = 0.67

所以，系统更倾向于推荐商品B给用户，因为它与用户偏好向量的内积更大，即匹配度更高。

✅ 延伸说明

在实际系统中：

• 用户向量可能是通过行为（点击、评分、浏览时间）学习得到；
• 商品向量则可能来自文本描述、图像、历史标签等编码；
• 内积可以用来快速进行批量推荐（例如用矩阵乘法实现 top-k 推荐）；
• 有时也会对向量进行归一化，使内积变成“余弦相似度”。