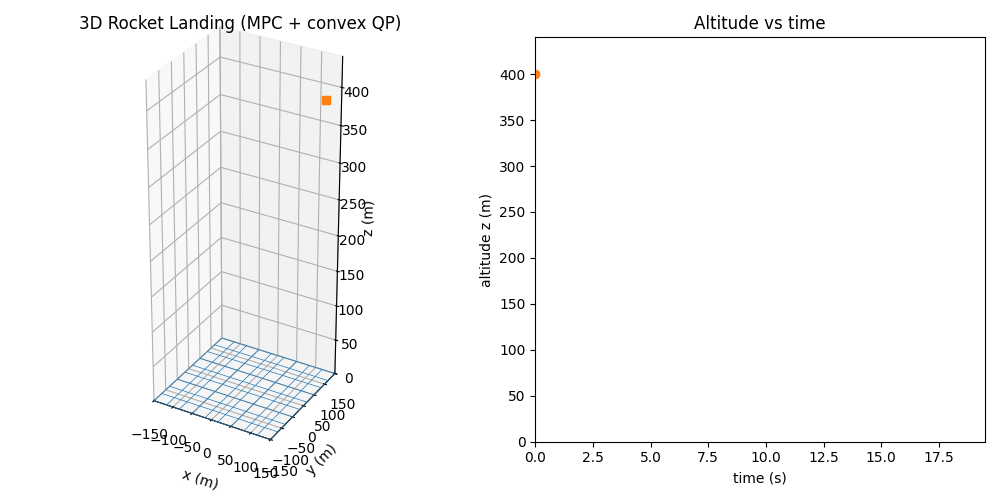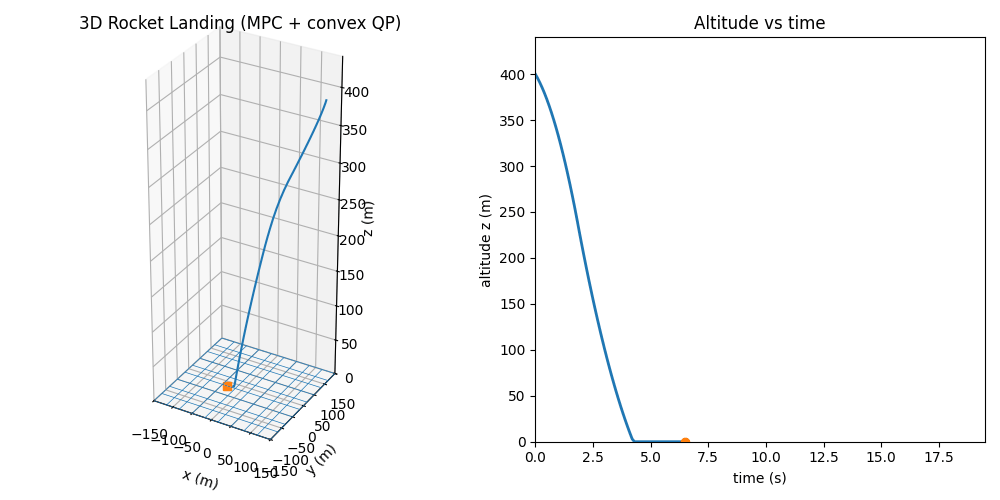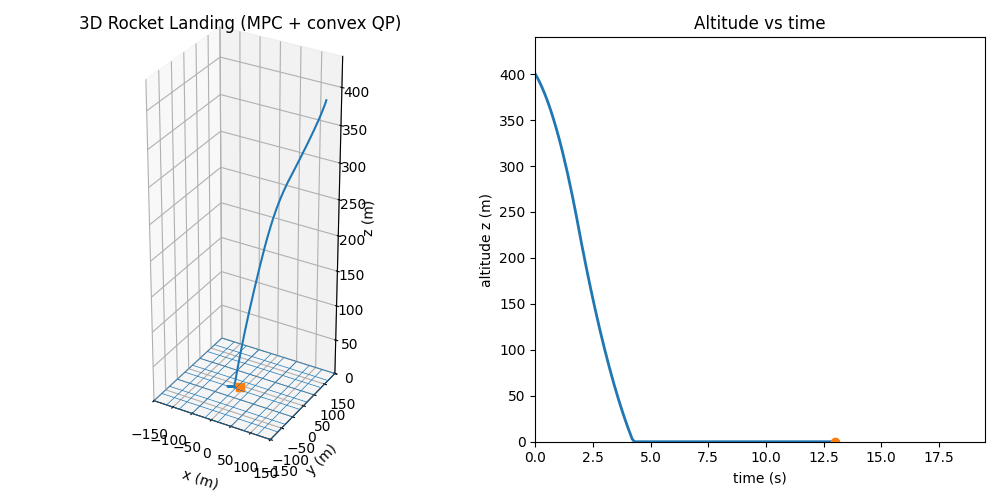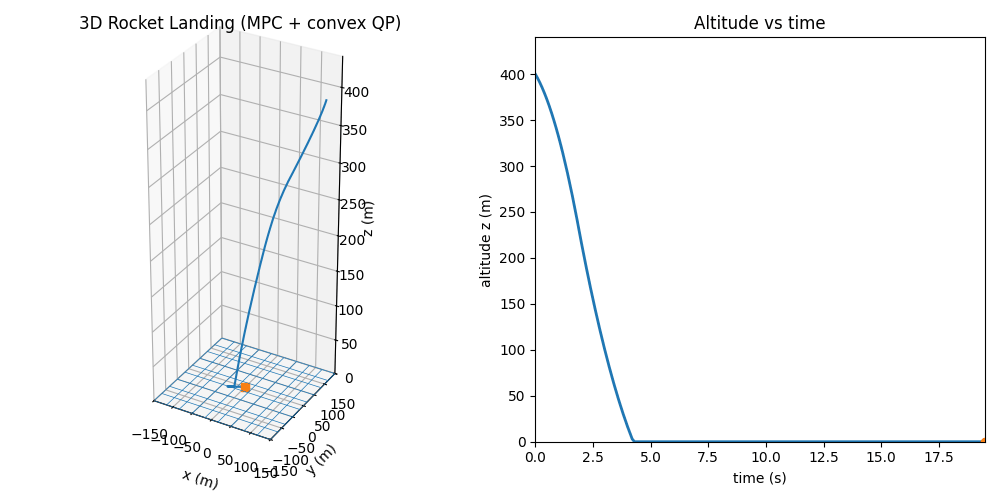
凸优化用在火箭助推器回收降落上,本质上是:把一个本来非常复杂、非线性的“怎么安全、节省燃料地降落”问题,改写成一类计算机能又快又稳定求解的凸优化问题,再在飞行电脑上实时解出来,指导推力和姿态控制。
一、火箭助推器回收降落要解决什么问题?
以猎鹰 9 一子级为例,从控制/优化角度看,助推器回收降落主要是一个有约束的最优控制问题:
· 状态变量:位置(x,y,z)、速度(vx,vy,vz)、姿态、角速度、剩余推进剂质量等;
· 控制变量:推力大小 T(t)、推力方向(发动机矢量)、栅格翼偏角、冷气体姿控等;
· 目标函数:通常是最小燃料消耗,或在给定燃料下最大化着陆安全裕度;
· 约束:包括动力学约束(刚体动力学和质量变化方程)、推力大小和偏转角约束、结构载荷约束、终端着陆条件约束、以及飞行走廊等安全区域约束。
把这些东西全放一起,就是一个大型的“带约束非线性最优控制问题”。
二、为什么要用凸优化而不是随便一个非线性优化?
传统非线性规划(NLP)或启发式搜索有几个致命问题:
1. 非凸问题会有很多局部最优解,往往不知道算出来的是不是全局最优;
2. 收敛时间和结果不可预测,迭代次数、是否收敛都不稳定;
3. 难以给出“肯定能找到可行解/最优解”的数学保证,这对安全关键系统是大问题。
而如果能把问题变成凸优化问题,情况就完全不同:目标和约束都是凸的时,任何局部最优都是全局最优;有成熟的内点法、二阶锥规划(SOCP)、线性规划(LP)求解器,收敛性和精度都有强理论保证,可以控制运算时间,机载实时求解成为可能。
三、原始的助推器着陆问题有哪些“非凸性”?
典型非凸来源包括:
1. 推力大小的“环状”约束:推力大小必须在 [T_min, T_max] 之间,是空心球壳/圆环,集合本身是非凸的;
2. 推力方向锥形限制:推力相对火箭纵轴偏转角有限制,涉及向量范数和比值,约束非线性、非凸;
3. 六自由度动力学和气动力的非线性;
4. 发动机开关、模式切换等“离散”决策,会引入混合整数和非凸结构。
直接把这些非凸约束塞给一个通用非线性规划求解器,很难保证既快又稳。
四、“无损凸化”是怎么把它“变成凸”的?
Acikmese、Blackmore 等人的关键思想是:通过引入新变量和适当的松弛,把非凸约束变成凸约束,然后证明这种松弛是“无损”的——凸问题的最优解一定满足原来的非凸约束,因此也是原问题的全局最优解。
典型步骤包括:
1. 时间离散化 + 动力学线性化:把连续最优控制问题离散成有限维线性系统。
2. 将推力“球壳”约束 [T_min, T_max] 松弛为球约束 [0, T_max]:先允许 0 到 T_min 这段本来不允许的区域,再通过目标函数和终端约束设计,证明最优解不会停在这段区域,从而松弛是无损的。
3. 将推力方向等限制写成二阶锥约束,例如范数形式 ‖a_k‖ ≤ b_k,这属于标准 SOCP 约束,具有凸性。
4. 通过严格证明:如果原非凸问题有可行解,松弛后的凸问题也有可行解,并且凸问题的最优解自动满足原来的非凸约束,因此同时是原问题的全局最优解。
五、在火箭回收中的实际使用方式:分层控制结构
在实际工程中,凸优化通常处于“轨迹规划 / 制导”这一层:
1. 最上层(轨迹/制导):每隔几十毫秒到几百毫秒,基于当前状态,构建一个有限预测时域的凸优化问题,求出未来几秒的“最优轨迹”和对应推力序列;
2. 中间层(姿态与推力控制):接收上层给出的期望推力矢量,用传统控制(如 PID/LQR/非线性控制)驱动发动机矢量、栅格翼和姿控系统去跟踪;
3. 底层(执行机构与故障管理):执行发动机节流、点火、舵机控制、落脚架展开,以及故障检测与冗余管理。
在这个结构中,凸优化负责“算清楚下一段时间内最佳的下落路径和推力计划”,下面的控制器负责让火箭沿着这条路径飞。
六、如何处理偏差和不确定性?
实际飞行中有风、发动机推力偏差、质量估计误差等不确定性,轨迹会和计划产生偏差。在凸优化框架下,可以通过鲁棒优化或机会约束等方式,把不确定性对轨迹偏差的统计要求纳入到优化问题中,比如:
· 要求“违反约束的概率不超过 1%”;
· 在最坏情形的扰动范围内,仍然保持落在安全着陆区。
七、复杂六自由度问题中的连续凸化
当加入六自由度刚体动力学、强气动力和状态触发约束等复杂因素时,单次线性化的凸问题可能不够精确。这时常用“连续凸化 / 递推凸化”(successive convexification):
1. 从一个初始轨迹出发,在其附近线性化动力学和约束,构造并求解一个凸优化问题;
2. 得到新的轨迹后,再以它为中心重新线性化,继续求解新的凸问题;
3. 经过若干次迭代,轨迹收敛到满足约束且性能优良的解。
八、CVXGEN 等代码生成工具如何保证实时性?
为了在机载计算机上实现毫秒级的求解时间,工程上通常使用如 CVXGEN 之类的凸优化代码生成工具:
1. 预先分析问题结构(变量规模、稀疏结构、约束类型等);
2. 自动生成针对该结构高度优化的 C 代码,避免运行时开销;
3. 在小规模问题上实现毫秒级或更快的求解性能。
九、直观几何图像的理解
可以把整个问题想象为:在状态空间里存在一个“安全走廊”,由位置、速度、姿态、质量等构成,推力约束和姿态约束限制了每一步可行的“方向和步长”。凸优化要做的,就是在这个走廊里,找到一条从“当前状态”走到“安全着陆状态”的最省油路径。
无损凸化保证:虽然原始问题中推力有“最小值”等非凸约束,但通过适当松弛和代价设计,最优解自然会贴在原来的物理边界上,而不会利用松弛出来的“非法区域”,所以松弛并不会引入假解。
十、一句话压缩总结
火箭助推器回收降落,从数学上看是一个“在复杂约束下求燃料最优、安全最优轨迹”的问题,其中许多约束天生是非凸的(最小推力、推力方向限制、六自由度非线性动力学等)。通过无损凸化和递推凸化等方法,可以把这类非凸最优控制问题转化为一系列凸优化问题,再用专门定制的凸优化求解器在机载计算机上实时求解,为每个控制周期生成“最佳下落路径”和推力指令,这构成了猎鹰 9 等现代可回收火箭实现高精度自动着陆的重要数学基础之一。
一、总体思路:我们到底想干什么?
想象一个极简版“猎鹰 9”竖直落地问题:
· 只有一个维度:竖直高度 h(t);
· 推力只能朝上;
· 我们希望从初始高度 h₀、向下的速度 v₀<0 开始,在给定时间 T_f 时刻“正好在地面、高度为 0,速度为 0(或很小)”;
· 同时尽可能少烧燃料。
从控制角度看,这就是一个“如何在有限时间内刹住并恰好落地”的最优控制问题。但真正麻烦的是——现实中的发动机有很多约束,比如最小推力、最大推力、推力方向限制等。这里我们先聚焦在“最小推力”这一点。
现实发动机通常是:要么关掉,要么推力在 [T_min, T_max] 区间内工作。于是,推力的可行集合是:
U = {0} ∪ [T_min, T_max], 0 < T_min < T_max
也就是说,(0, T_min) 这段被“挖空”了,这个集合本身是非凸的,这也是我们需要“凸化”的根本原因。
二、一维垂直降落的玩具动力学模型
先写一个极简动力学(暂不考虑质量变化):
· 高度 h(t):向上为正;
· 速度 v(t):向上为正;
· 控制量为推力 T(t),向上;
动力学方程可以写成:
ẋ₁ = v(t)
ẋ₂ = T(t)/m − g
其中 m 暂时看作常数,g 为重力加速度,向下(所以是 “−g”)。
边界条件为:
· 初始:h(0) = h₀, v(0) = v₀;
· 终端:h(T_f) = 0, v(T_f) = 0(理想软着陆)。
发动机推力约束为:
· 要么关机:T(t) = 0;
· 要么开机:T(t) ∈ [T_min, T_max]。
目标函数可简单设为:
min ∫₀^{T_f} T(t) dt
可以理解为总推力积分(总冲量),与燃料消耗线性相关。
三、为什么这个问题是“非凸”的?
从凸优化视角看,要满足两点:
1)决策变量的可行集合要是凸集;
2)目标函数和约束在该集合上是凸的(目标凸、等式约束仿射、不等式约束定义凸集)。
在这里,决策变量是控制函数 T(t) 的轨迹:
· 目标 ∫ T(t) dt 是线性的,因此是凸的;
· 动力学约束是线性的微分方程(离散后是线性等式);
· T ≤ T_max、T ≥ 0 这类约束都是凸的(线性不等式);
· 但是核心问题在于:T(t) ∈ {0} ∪ [T_min, T_max],这是“一个点 + 一个区间”的并集,明显不是凸集。
因此,即使动力学是线性的、目标是线性的,只要控制域是这样的并集,这个最优控制问题仍然是非凸的。
四、第一步:时间离散化,把最优控制变成有限维优化
为了用通用优化器(包括凸优化器),我们通常把时间区间 [0, T_f] 离散化:
· 把 [0, T_f] 切成 N 个等长时间步,步长 Δt = T_f / N;
· 用离散时刻 k = 0,1,…,N 表示。
定义离散变量:
· 高度 h_k ≈ h(kΔt);
· 速度 v_k ≈ v(kΔt);
· 推力 T_k ≈ T(kΔt)。
用前向欧拉法离散动力学:
h_{k+1} = h_k + Δt · v_k
v_{k+1} = v_k + Δt · (T_k/m − g)
边界条件:
· h_0 = h₀, v_0 = v₀;
· h_N = 0, v_N = 0。
离散后推力约束:
T_k ∈ {0} ∪ [T_min, T_max], k = 0,…,N−1
目标函数离散为:
min Σ_{k=0}^{N−1} T_k Δt
如果我们暂时忽略“最小推力”和“开关结构”,只保留 0 ≤ T_k ≤ T_max,那么整个问题就变成了一个线性规划(LP):
· 目标 Σ T_k Δt 线性;
· 动力学约束线性等式;
· box 约束线性不等式;
· 终端约束线性等式。
这是完全凸的。关键问题是:能不能把原来的非凸集合 {0} ∪ [T_min, T_max] 松弛成 [0, T_max],同时不丢失最优解?
五、“无损凸化”:把非凸推力集合松弛为凸集合
我们考虑如下“松弛”:
· 原约束:T_k ∈ {0} ∪ [T_min, T_max];
· 松弛约束:0 ≤ T_k ≤ T_max。
直觉上,松弛后可行集合更大,所以松弛问题的最优值不大于原问题的最优值。关键是要证明:在松弛问题的最优解中,不会出现 0 < T_k < T_min 的情况,也就是说,最优解不会用到那一段被“新放开的区域”。
类比现实生活:在“最小化燃料”的前提下,与其一直半踩油门,不如在该刹车的时候踩一脚实在的。在本问题结构下,可以构造证明:任何出现在 (0, T_min) 区间内的推力使用,都可以用“在某些时刻关机 + 在某些时刻用不小于 T_min 的推力”替代,且不增加总推力积分、不破坏终端条件。
更正式地说:在线性动力学 + 线性目标下,系统对推力序列的响应具有某种“线性可加性”,使得小推力长时间作用可以被等效为大推力短时间作用。通过一类“挤压式”的构造,可以证明松弛问题的最优解完全可以选择 T_k ∈ {0} ∪ [T_min, T_max],从而松弛是无损的(lossless)。
六、引入发动机模式变量:从“半连续输入”到凸优化
如果进一步形式化,可以在离散问题中引入一个“发动机开关变量” σ_k:
· σ_k = 0:发动机关机;
· σ_k = 1:发动机开机。
原来的推力约束可以等价写成:
σ_k ∈ {0,1}
T_k ≥ σ_k T_min
T_k ≤ σ_k T_max
这时问题变成了带二元变量的混合整数规划(MILP),更加非凸。
凸化的关键一步是:把 σ_k ∈ {0,1} 放松为连续变量 0 ≤ σ_k ≤ 1。这样配合 T_k ≥ σ_k T_min、T_k ≤ σ_k T_max,所有约束都是线性的,问题变成纯凸(甚至是 LP 或 QP)。随后,再通过与前一节类似的结构性证明,说明在最优解中 σ_k 会自动跑到 0 或 1,因此这一放松也是无损的。
七、把它正式写成一个“凸优化问题”的标准形式
经过上述离散化和松弛,可以得到一个典型的凸优化问题,变量包括:
· 状态:{h_k, v_k}, k = 0,…,N;
· 控制:{T_k, σ_k}, k = 0,…,N−1。
目标函数:
min Σ_{k=0}^{N−1} T_k Δt
约束包括:
1)初值约束:h_0 = h₀, v_0 = v₀;
2)线性动力学约束:
h_{k+1} = h_k + Δt · v_k
v_{k+1} = v_k + Δt · (T_k/m − g)
3)终端约束:h_N = 0, v_N = 0;
4)推力和开关变量约束(松弛后):
0 ≤ σ_k ≤ 1
T_k ≥ σ_k T_min
T_k ≤ σ_k T_max
T_k ≥ 0
这是一个标准的凸优化问题(通常是 LP 或 QP)。结合“无损凸化”的证明,我们知道最优解自动满足 σ_k ∈ {0,1},从而也满足原始物理推力约束。
八、回到“火箭助推器回收”的现实意义
上面这一大圈,是在一个 1D 玩具模型里演示了几件事:
1)原始问题因为推力集合 {0} ∪ [T_min, T_max] 的缘故是非凸的;
2)通过引入辅助变量和松弛,可以把它改写成一个凸优化问题;
3)在适当设计目标与约束的情况下,松弛是无损的,凸问题的最优解自然满足原来的物理约束;
4)一旦变成凸问题,就可以用成熟的 convex solver(LP/QP/SOCP)做实时求解;
5)在真正的火箭中,这一套通常被放在“轨迹规划/制导”层,下面再叠加姿态控制和执行机构控制等模块。
如果把模型从 1D 扩展到 2D/3D,推力变成向量 T⃗_k,推力方向、偏转角等约束可以写成二阶锥约束(例如 ‖T⊥‖ ≤ tan(θ_max)·T_z),整个问题自然升级为二阶锥规划(SOCP)。这就是很多火箭回收论文里提到的“基于 SOCP 的轨迹优化”的来历。
在工程实践中,还会叠加非线性气动力、六自由度刚体动力学等,这时通常会在这一套“凸化框架”上使用连续凸化(successive convexification),即:选一个初始轨迹,线性化得到一个凸问题,求解得到新轨迹,再围绕新轨迹继续线性化、求解,迭代若干次直到收敛。
总之,凸优化在火箭助推器回收降落中的核心作用,是把一个原本非凸、难以直接求解的最优控制问题,通过精心设计的松弛和重写,变成一系列可由可靠、实时的凸优化求解器解决的问题,从而实现高精度、可证明、可工程落地的自动着陆控制。