论文Less is More: Recursive Reasoning with Tiny Networks针对在数独、迷宫、ARC-AGI 等“硬推理”任务上,传统大语言模型(LLMs)即便结合链式思维(CoT)与测试时计算(TTC)仍难以达成人类级表现的问题,提出了一个显著更简洁且更强泛化的递归推理范式——Tiny Recursive Model(TRM)。TRM用单个仅两层的小网络,通过对“潜在推理状态 z”与“当前解 y”交替递归更新的方式,在小数据(~1K)和小模型(~7M 参数)条件下,超越了使用两套网络、依赖固定点近似与 Q-learning 式 ACT 的层级递归模型 HRM,并在多个基准上优于大量参数级别远超的 LLM。作者报告:Sudoku-Extreme 87.4%、Maze-Hard 85.3%、ARC-AGI-1 44.6%、ARC-AGI-2 7.8%,其中对比 HRM 的 55.0%、74.5%、40.3%、5.0%均有提升。
论文作者为Alexia Jolicoeur-Martineau,来自Samsung。
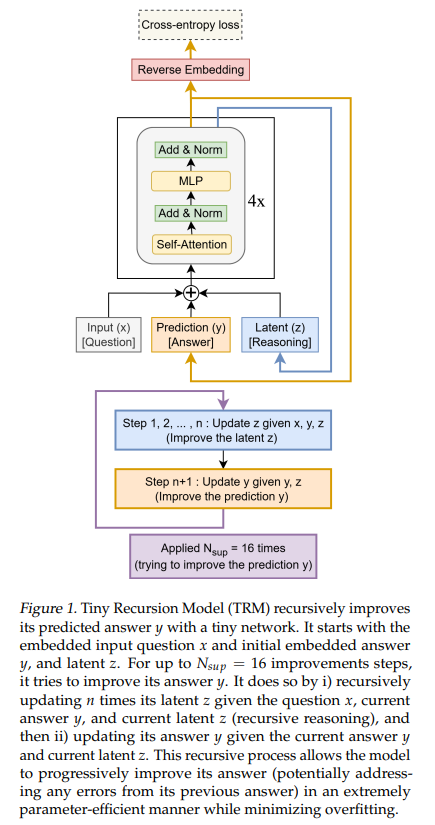
一、背景:HRM 的理念与瓶颈
HRM(Hierarchical Reasoning Model)提出以两套小网络在不同频率(低层 fL 高频、 高层 fH 低频)递归更新两个潜变量(zL、zH),并在深度监督(deep supervision)下多轮改进答案;训练时引入自适应计算时间 ACT以早停;为降低内存,采用隐函数定理(IFT)+ 一步梯度近似,只对最后少量递归步回传梯度。该方法虽在 Sudoku、Maze、ARC-AGI 有突破,但存在三类关键问题:
1)固定点假设存疑:实际递归步数小(常用 n=2、T=2),难保证已达固定点却使用一步梯度近似;论文也援引第三方分析指出,深度监督而非“层级递归”似是主要收益来源。
2)ACT 训练成本偏高:采用 Q-learning 形式的 halt/continue 信号,其中“continue”分支需要额外一次完整前向,导致每步优化需两次前向。
3)生物学隐喻复杂且难以做因果归因:两层级、两潜变量的设计更像是工程设定,缺乏清晰简化解释。
二、TRM 的思想重构:把“层级”化繁为简
TRM抛弃“二网络二层级”的生物学隐喻,转而给出更直观的二变量解释:
- y:当前(嵌入后的)候选解;
- z:不可直接解码的潜在推理状态(类似“可被迭代的思考痕迹/中间证据”)。
递归过程在每个“改进回合”里分两步交替:
1)用 (x,y,z) 更新 z(“先想清楚”);
2)用 (y,z) 更新 y(“再改答案”)。
关键点:
- 只用一个两层网络同时承担“更新 z”和“更新 y”的功能;是否包含输入 x 决定子任务(更新 z 的分支读入 x,更新 y 的分支不读入 x)。
- 在深度监督下,模型学会“接过任意 (y,z)”再改进一点,因此可以先做 T−1 次无梯度递归靠近解面,再做 1 次带梯度递归进行学习,无需 IFT/一步近似。
- ACT 简化:只保留“是否已足够好可停”的单一二分类(与“预测正确”相关联),去掉“continue”损失,从而避免额外前向。
- EMA(指数滑动平均)稳定训练,尤其小数据场景下显著抑制过拟合发散。
三、算法机制与训练细节(直观解读)
1)递归单元(latent recursion)
- 重复 n 次:z←net(x,y,z);
- 然后一次:y←net(y,z);
这构成一次“完整递归过程(full recursion)”。
2)深度监督(Nsup ≤ 16)
- 每个监督步:先跑 T−1 次无梯度完整递归,进一步“暖机”(y,z);再跑 1 次带梯度完整递归并计算主损失(交叉熵 w.r.t. 真值)。
- 训练时附带一个halt 概率(BCE 损失)→ 若“看起来已正确”,可早停继续下一个样本,从而在固定总迭代预算下覆盖更多样本。
3)为什么只要两个特征(y 与 z)就够?
- 若没有 y,模型被迫在 z 内同时保存“解”和“推理”,冲突大、难训练;
- 若把 z 再拆多份(多尺度 z),引入冗余耦合反而降低泛化;
- 实验证明“两变量最佳”,单 z 或多 z 均显著掉点。
四、与 HRM 的系统性对比(设计→训练→代价)
| 维度 | HRM | TRM |
|---|---|---|
| 结构 | 两网络(fL 高频、fH 低频);zL、zH | 单网络;“y=候选解、z=潜在推理” |
| 递归回传 | 倚赖 IFT 的“一步梯度近似”,仅末两步回传 | 对完整递归回传梯度,无需固定点假设 |
| 深度监督 | 是(Nsup≤16) | 是(同) |
| ACT | Q-learning:halt/continue,需额外一次前向 | 仅 halt 二分类,不需额外前向 |
| 归纳偏置 | 生物层级解释 | 任务直觉解释(先想后改) |
| 参数规模 | 典型 27M | 典型 5–7M(2 层) |
| 训练稳定性 | 容易过拟合并崩溃 | 引入 EMA 显著稳定 |
五、实验结果与消融结论
1)总体成绩(直接监督,小样本)
- Sudoku-Extreme:TRM-MLP 87.4%(HRM 55.0%)
- Maze-Hard(30×30 长上下文):TRM-Att 85.3%(HRM 74.5%)
- ARC-AGI-1:TRM-Att 44.6%(HRM 40.3%)
- ARC-AGI-2:TRM-Att 7.8%(HRM 5.0%)
TRM 在参数更小(~7M)下普遍优于 HRM(~27M)。
2)自注意力 vs. MLP Mixer 式序列 MLP
- 小且固定上下文(如 9×9 数独):用 MLP 代自注意力更优(87.4% vs 74.7%),因 L≤D 时 MLP 以更少参数覆盖全序列交互。
- 较大网格(30×30 迷宫、ARC):自注意力更合适,MLP 反而欠拟合/过拟合失衡。
3)层数与递归步数(“少即是多”)
- 增加层数(4 层)会泛化下降(79.5%),而2 层 + 增加递归最优(87.4%),说明在小数据 regime 下,把容量转移到“深递归/深监督”比“加层数”更能抑制过拟合。
4)EMA 与 ACT 简化
- 去掉 EMA 会显著掉点(79.9%);
- 将 ACT 从 Q-learning(两前向)改为“仅 halt”不影响泛化,还节省计算。
5)特征形态消融
- 单 z 或多尺度 z(把每次递归产出的 z_i 都跨步携带)都劣于“两变量(y,z)”基线,验证“二而不繁”的优势。
六、方法直觉与理论思考
1)为何深递归 + 深监督能涨泛化?
在小数据/小模型下,直接“加宽加深”易过拟合;反之,通过多次“无梯度自校正”把状态带到更“接近可解流形”的区域,再在最后一次递归进行学习,等价于“把梯度投射到更有信息的局部邻域”,起到正则化与优化景观重塑的效果。
2)y 与 z 的角色分离
- y 外显、可解码且被判定对错;z 内隐、累积“解决该题的思考线索”。两者分离避免信息内卷与冲突存储,让“想”(z)与“改”(y)职能清晰,递归效率更高。
3)为何无须固定点与一步近似
TRM 不是追求严格固定点,而是把一次“完整递归过程”视为可学习的改进算子,直接对其求梯度;这既规避了固定点是否存在/可收敛的前提,又保留了“多次无梯度改进”的便宜性。
七、工程落地要点(复现指南级摘要)
- 网络:2 层(含自注意力或序列 MLP,视任务上下文长度而定),隐藏维 512;
- 递归超参:推荐 T=3、n=6(Sudoku 最优点),注意 n 过大需考虑显存(TRM 对完整递归回传);
- 深度监督:Nsup ≤ 16;训练时按监督步循环,“T−1 次无梯度 + 1 次有梯度”;
- ACT:仅训练时预测 halt 概率(BCE),为覆盖更多样本可早停;测试时通常跑满 Nsup;
- 优化:AdamW(β1=0.9, β2=0.95,warmup 2K)、稳定 softmax(stable-max)、适度权衰减;EMA=0.999;
- 数据增强:Sudoku(规则保持的洗牌 ×1000)、Maze(D8 群 8 种变换)、ARC(颜色置换+平移+ D8 ×1000),并对每次增强分配特定嵌入以减小数据稀疏。
八、适用边界与开放问题
- 任务依赖:当网格/上下文较大时,自注意力优于序列 MLP;在固定小网格任务中,序列 MLP 更经济高效。
- 规模律缺失:作者指出仍需建立“递归推理网络的规模律”(层数、递归步数、宽度与数据量之间的最优配比)。
- 生成式扩展:当前为判别式/监督式一次一答;现实中多解场景普遍,值得把 TRM 扩展为生成式(e.g., 采样多条推理轨迹/多解)。
- 理论阐释:为何“深递归+小网络”在小数据下显著胜于“深大网络”的系统性理论仍欠缺。
九、与 LLM(CoT/TTC)的关系与启示
- TRM 并非基于大语料预训练,而是小样本直接监督;其强项在结构性推理与几何变换不变性可通过数据增强与递归操作显式注入。
- 对 LLM 的启示:与其在推理时“扩展采样深度”(多数投票),不如在模型结构中内生“先思后改”的递归算子,用少量参数获得可复制的稳定推理过程。
- 在工业/边缘推理场景里,TRM 风格的“小而递归”可能更具成本/能效优势。
十、总体评价
TRM 以更少的层数、更小的参数、更简洁的训练机制,在多个硬推理基准上实现了更强的泛化,并用一套直观的“y(解)/z(思考)”二变量解释,澄清了 HRM 中“层级递归”的真实有效因素:深度监督 + 多次无梯度自校正 + 完整递归回传。这为“用小网络做大推理”指明了清晰、可实现的技术路径。