综述论文Machine Learning with Physics Knowledge for Prediction: A Survey(《结合物理知识的机器学习预测方法概述》)深入探讨了如何将物理学知识与机器学习相结合,目的是提高对科学和工业系统的预测能力,尤其是在涉及偏微分方程(PDEs)的背景中。通过引入物理知识,机器学习模型可以在有限的数据条件下获得更加鲁棒和可靠的表现。这种结合可以解决传统机器学习方法在数据稀缺场景中的局限,同时提升模型对复杂物理系统的理解和预测能力。
论文作者为Joe Watson, Chen Song, Oliver Weeger, Theo Gruner, An T. Le, Kay Hansel, Ahmed Hendawy, Oleg Arenz, Will Trojak, Miles Cranmer, Carlo D’Eramo, Fabian Bülow, Tanmay Goyal, Jan Peters, Martin W. Hoffman,来自以下多个机构:
- Department of Computer Science, Technical University of Darmstadt, Germany
- Systems AI for Robot Learning, German Research Center for AI (DFKI), Germany
- Hessian Center for Artificial Intelligence (hessian.AI), Germany
- Center for Artificial Intelligence and Data Science, University of Würzburg, Germany
- Centre for Cognitive Science, Technical University of Darmstadt, Germany
- ABB Corporate Research Center, Mannheim, Germany
- Department of Mechanical Engineering, Technical University of Darmstadt, Germany
- IBM Research UKI, United Kingdom
- Data Intensive Science, University of Cambridge, United Kingdon
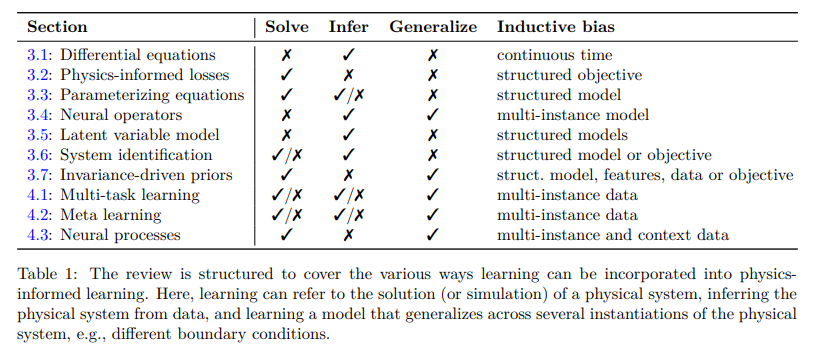
以下为论文概要内容:
1. 研究背景与动机
科学与工程领域的进展依赖于对自然规律的探索和对物理现象的精确建模。然而,传统的物理建模方法常常通过简化和抽象,未能充分捕捉系统的全部复杂性,尤其在面对高度非线性和复杂的多尺度系统时。例如,天气系统和生物过程等复杂系统的精确建模是极具挑战的。与此同时,机器学习技术的发展提供了一种新的工具,可以利用大规模数据驱动的方法来建模和预测物理系统的行为。特别是深度学习和神经网络的出现,使得通过大规模数据训练参数化模型来替代传统基于物理方程的预测成为可能。
然而,纯粹的数据驱动方法也有其不足,尤其是在数据有限的场景下。物理驱动的机器学习方法则提供了一条途径,将数百年来的科学研究成果与现代机器学习的灵活性相结合,从而增强模型的鲁棒性、可靠性以及小样本条件下的学习能力。这种结合能够在不完全依赖大数据的情况下,利用已有的物理知识引导模型训练,使得模型能够有效学习即使数据相对较少或质量欠佳的情形下依旧能表现出色。
2. 结合物理知识的机器学习方法
本论文将物理知识与机器学习结合的方法分为两个部分进行探讨:
- 第一部分介绍了在模型架构层面如何通过物理知识增强机器学习,例如目标函数的改进、结构化预测模型和数据增强等。
- 第二部分则探讨了如何通过数据本身来引入物理知识,利用多任务学习、元学习和上下文学习等数据驱动的方法,将物理先验嵌入到模型的训练中。
2.1 物理知识在模型架构中的融合
结合物理知识到机器学习的模型架构中有多种方式,例如:
- 目标函数中的物理驱动约束:通过将物理知识融入到目标函数中,使得模型在训练过程中能够遵循物理规律。例如,物理驱动的神经网络(Physics-Informed Neural Networks, PINNs)通过将偏微分方程作为目标函数的一部分,使模型在拟合数据的同时,也满足物理定律。
- 结构化预测模型:这种方法通过引入物理先验,将物理学的知识转化为模型结构的一部分,例如通过添加约束条件或特定的模型结构,使得模型具备更好的泛化能力。
- 数据增强:数据增强是一种结合物理知识的策略,目的是在有限数据条件下提升模型的性能。例如,在数据生成过程中,利用物理规律来构造虚拟的数据点,使得模型对物理系统的理解更为深入。
2.2 数据驱动的物理知识结合
对于许多物理现象,数据本身可以被视为物理知识的承载。通过合理利用这些数据,可以将物理知识与机器学习进行更加深度的融合。例如:
- 多任务学习(Multi-task Learning):通过对多个相关任务进行联合学习,模型可以在不同任务间共享物理知识,提高整体的学习效率。
- 元学习(Meta-learning):元学习方法可以通过在不同物理环境下训练模型,使其具备快速适应新环境的能力,从而使模型能够在面对不同物理系统时保持良好的表现。
- 神经算子(Neural Operators):神经算子用于学习输入参数到系统解之间的整体映射。这种方法可以有效地学习不同边界条件下偏微分方程的解,从而具备较强的泛化能力,特别是在跨多个物理系统实例进行泛化时表现突出。
3. 关键方法的介绍
在论文中,作者详细讨论了几种主要方法,这些方法通过不同的方式将物理知识融入到机器学习模型中,以应对复杂的物理预测任务。
3.1 物理驱动的神经网络(PINNs)
物理驱动的神经网络(PINNs)是结合物理知识进行预测的一种典型方法。PINNs通过将偏微分方程(PDEs)作为损失函数的一部分,将物理约束条件直接应用于神经网络中。具体来说,PINNs的目标函数包括两个部分:
- 物理残差损失(Physics Residual Loss):通过计算物理方程在网络预测解处的残差,并将其最小化,使得网络预测的解满足物理约束。
- 边界条件损失(Boundary Condition Loss):通过对边界条件进行约束,使得模型在边界处的预测符合物理定律。
PINNs的方法有助于解决在数据不足时预测精度低的问题,因为通过物理方程的约束,模型可以在没有足够数据的情况下仍然进行合理的预测。然而,在实际应用中,PINNs的训练存在一些挑战,包括如何平衡多目标损失、如何优化采样策略以减少误差传播等。
3.2 神经微分方程(Neural ODE)
神经微分方程(Neural ODE)是一种通过将连续时间积分引入模型的方式,来增强其对时间序列的建模能力。神经ODE的优势在于它可以对任意时间点进行预测,而不需要固定的时间步长。这种方法特别适用于不规则时间间隔的数据。为了计算模型的梯度,神经ODE采用了一种称为伴随方法(adjoint method)的技术,该方法通过反向时间积分来高效地计算模型参数的梯度,使得内存开销显著降低。
3.3 拉格朗日与哈密顿神经网络(LNNs和HNNs)
- 拉格朗日神经网络(Lagrangian Neural Networks, LNNs):LNNs通过结合拉格朗日力学中的能量守恒等物理定律,将系统的运动方程引入到神经网络的优化过程中。通过这种方式,LNNs可以更好地捕捉物理系统的动态行为,尤其是在涉及机械系统的建模中表现出色。
- 哈密顿神经网络(Hamiltonian Neural Networks, HNNs):HNNs通过对哈密顿方程的建模,确保模型在相空间中的能量守恒特性。这种方法通常用于保守系统的建模,例如经典力学系统。
3.4 神经算子(Neural Operators)
神经算子是一种用于学习输入参数到解之间映射的方法,可以看作是一种泛化的网络架构,其目标是学习从函数空间到解空间的映射。通过这种方法,神经算子可以实现跨越不同物理条件的泛化能力,而不仅仅是求解特定条件下的PDE。常见的神经算子方法包括:
- DeepONet:通过学习输入函数的有限维表示,DeepONet可以有效地捕捉输入与输出之间的非线性关系。
- 傅里叶神经算子(Fourier Neural Operators, FNOs):FNOs通过将积分核算子表示为傅里叶变换,从而大大降低了计算复杂度,使得模型能够高效处理高维数据。
3.5 参数化的代数结构与隐变量模型
结合物理知识的另一个重要方法是通过参数化代数结构来描述系统的物理约束。例如,通过拉格朗日和哈密顿力学中的约束条件,将系统动态表示为相应的代数表达式。这种方法有助于提高模型的学习效率和计算效率,并在动力学系统的建模中表现出色。此外,隐变量模型(Latent Variable Models, LVM)假设观测数据由未观测的潜在过程生成,从而通过推断这些潜在变量来简化复杂系统的学习问题。
4. 工业应用与挑战
物理驱动的机器学习在工业中的应用非常广泛。例如:
- 天气预测:利用神经算子和多任务学习等方法可以对天气系统的复杂动态进行预测,这些方法在处理具有多重空间和时间尺度的混沌系统方面表现优异。
- 故障检测:在工业生产中,结合物理模型与实时测量数据,模型可以对系统的运行状态进行评估并预测潜在故障,从而确保系统的可靠性。
- 逆问题求解:在许多物理系统中,通过已知的输出条件,模型可以推断出系统所需的输入条件。这些方法在物理驱动的设计和系统操作中具有重要意义。
5. 当前的挑战与未来的发展方向
尽管物理驱动的机器学习方法具有许多优势,但在实现过程中仍存在不少挑战:
- 训练稳定性:由于PINNs等方法的目标函数中包含自约束项,因此模型在训练过程中需要与自身进行回归,直到达到自洽。这种训练过程容易出现不稳定的问题,可能导致优化失败。
- 多目标损失的权重选择:如何为每个损失项选择合适的权重对模型的训练效果影响显著。选择不当可能导致某些目标项的权重过大,影响整体的训练稳定性。
- 采样策略的优化:在PINNs的训练中,如何选择积分域内的采样点是一个关键问题。传统的数值积分方法计算开销大,而蒙特卡罗采样方法虽然灵活,但目标估计的方差较大。因此,提出了许多改进的采样策略,如重要性采样和主动采样,以提高训练的效率和效果。
6. 总结
物理驱动的机器学习方法通过将物理知识嵌入到机器学习模型中,显著增强了模型的预测能力,特别是在数据稀缺的情况下表现尤为突出。通过不同的方式结合物理知识,如物理驱动的目标函数、结构化的模型架构和数据增强等,机器学习模型不仅提高了对复杂物理系统的理解能力,还提升了其在工业应用中的实用性和可靠性。
未来的研究方向可以包括以下几个方面:
- 提升训练效率与稳定性:开发新的优化方法,以减少训练过程中的不稳定性,尤其是在涉及高维空间和复杂物理约束的情况下。
- 更多元的物理知识结合方式:探索物理学与机器学习更深层次的结合方式,例如更灵活的神经算子、更广泛的元学习方法等。
- 更高效的工业应用转化:将这些物理驱动的机器学习方法应用于更多的工业领域,例如自动化控制、能源优化、结构健康监测等,以解决实际生产中的复杂问题。