用物理信息神经网络（PINNs）求解非稳态麦克斯韦方程

论文PINNs for Solving Unsteady Maxwell’s Equations: Convergence Issues and Comparative Assessment with Compact Schemes主要研究使用物理信息神经网络（PINNs）求解非稳态麦克斯韦方程的性能，并与传统数值方法（如FDTD和Pade紧致格式）进行对比，重点分析其收敛性问题及其背后的训练机制。

论文作者为Gal G. Shaviner, Hemanth Chandravamsi, Shimon Pisnoy, Ziv Chen, Steven H. Frankel，来自Israel Institute of Technology。

麦克斯韦方程是描述电磁场行为的基础方程，广泛应用于光学、无线通信、电路等领域。尽管已有许多数值方法（如有限差分时域法FDTD、有限元法FEM等）用于近似求解这些方程，但它们通常受制于“维度灾难”带来的计算复杂度激增，此外，在处理复杂几何、稀疏或噪声数据时也存在困难。

为此，近年来提出的物理信息神经网络（PINNs）为求解偏微分方程提供了一种新的思路。PINNs将物理方程作为损失函数项直接嵌入神经网络训练过程，实现了无网格（mesh-free）的求解框架。但在面对非稳态、波动性强或具有高频特征的系统时，PINNs通常收敛速度慢、容易陷入训练病态问题。

本论文回答以下三个关键问题：

作者采用的是无源区域下的标准麦克斯韦方程形式（无自由电荷和电流），特别地，着重于二维情况下的电场 E_z 与磁场 H_x,H_y的耦合系统。该系统具有强非线性与高阶导数特征，数值求解时对空间与时间分辨率均提出较高要求。

神经网络架构
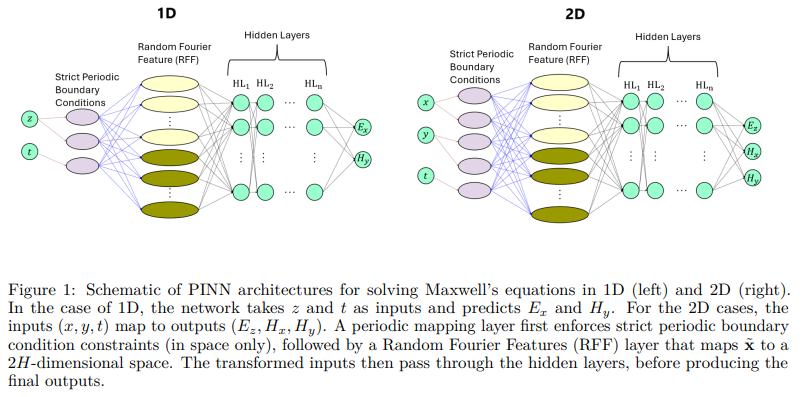
采用全连接前馈神经网络，将输入 (x,y,t) 映射为输出 (E_z, H_x, H_y)。为应对高频难以学习的问题，引入了以下关键技术：
- 周期映射与Random Fourier Features（RFF）：将输入先进行空间周期变换，再通过RFF映射到高维空间，有助于缓解神经网络的频谱偏差（即更偏好学习低频解）。
- Random Weight Factorization（RWF）：初始化权重以增强梯度传播，促进训练稳定性。
- 因果性训练（Causality Training）：引导网络优先学习初期时间步的物理过程，避免过早拟合错误的后期解。
损失函数构成
总损失由三部分组成：
- 初始条件损失 L_IC
- 边界条件损失 L_BC（对于周期边界问题可省略）
- 残差损失 L_res，用于约束网络输出满足麦克斯韦方程
因果性加权机制
通过时间步长的权重 w_i 控制训练注意力的分布，从而实现对早期动态的优先拟合，提升整体稳定性与物理一致性。

作者设计了三个经典电磁场问题，对PINNs与传统方法的性能进行对比分析：

一维高斯脉冲传播问题
- 在自由空间中传播的时间衰减电场脉冲，设定清晰的初始与边界条件。
- 对比结果显示，FDTD与Pade方法在波动区间易产生数值震荡，而PINNs能够更精确地捕捉电场的陡变边界，且无明显震荡。
- 证明PINNs在处理短时冲击问题时具有更高的稳定性与解析能力。
二维周期盒中的高斯脉冲演化
- 实现了空间与时间双周期性建模，使用周期映射和RFF对PINNs架构进行增强。
- 进行了详细的消融实验，逐一去除RFF、周期性、因果性训练等组件。结果显示，RFF是最关键的因素，其次是空间周期性，而因果性训练则有助于提升稳定性。
- 最优模型在空间 L² 误差上远优于其他配置，且误差在时间上分布更均匀。
二维高斯脉冲与介电介质相互作用
- 在介电常数非均匀（ε = 1 和 ε = 4）的情况下测试PINNs鲁棒性。
- 出现新现象：若强制加入空间周期性，反而会降低解的准确性，尤其是在介质边界附近产生较大误差。
- 去除空间周期性并保留RFF与因果性训练的配置，反而达到了最优精度，表明应当根据问题物理特性调整PINNs架构。

为了分析PINNs在时空维度上的收敛特性，作者采用了经验神经切线核（NTK）理论。其核心思想是通过计算NTK矩阵的特征值之和估计局部学习速度（收敛率）：

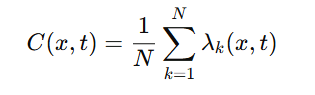
分析结果表明：