论文Pretraining Codomain Attention Neural Operators for Solving Multiphysics PDEs提出新型架构Codomain Attention Neural Operator (CoDA-NO)。CoDA-NO通过引入值域注意力机制和自监督预训练策略,为多物理场PDE求解提供了一种全新的解决方案。该架构能够有效处理具有复杂交互作用的多物理场问题,并通过少样本微调实现快速适应。CoDA-NO的表现优于传统的数值方法和现有的神经网络方法,尤其在数据稀缺和多物理场问题中展现出较强的能力。
论文作者为,来自Md Ashiqur Rahman, Robert Joseph George, Mogab Elleithy, Daniel Leibovici, Zongyi Li, Boris Bonev, Colin White, Julius Berner, Raymond A. Yeh, Jean Kossaifi, Kamyar Azizzadenesheli, Anima Anandkumar,来自Purdue University, Caltech, NVIDIA。
一、背景与问题
在许多科学和工程问题中,偏微分方程(PDE)用来描述物理现象,如流体动力学、波传播、材料变形等。尤其在涉及多个物理过程相互作用的多物理场(multiphysics)问题中,多个PDE系统需要耦合求解。传统的数值方法,如有限差分法、有限元法等,虽然能够解决这些问题,但它们通常面临计算量大、内存需求高、难以应对复杂几何形状和高分辨率数据的问题:
- 耦合PDE问题的复杂性:多物理场问题涉及多个耦合的物理方程,这些方程之间的复杂交互使得求解过程更为困难,尤其是当需要考虑复杂几何形状和边界条件时。
- 数据稀缺问题:传统数值方法需要大量的高分辨率数据进行训练,但获取这些数据不仅成本高,还需要大量计算资源。在一些多物理场问题中,尤其是模拟仿真非常昂贵,获取的训练数据常常十分有限。
现有的神经网络方法,如神经算子(Neural Operators),虽然能够在一定程度上取代传统数值方法,但在处理多物理场耦合问题时存在显著不足,主要表现为:
- 无法处理不同物理变量和不同网格分辨率的多物理场耦合问题。
- 无法有效利用现有的有限数据进行预训练和迁移学习。
二、CoDA-NO架构:Codomain Attention Neural Operator
为了应对上述挑战,论文提出了一种新型的架构——CoDA-NO(Codomain Attention Neural Operator)。该方法通过引入值域注意力机制(codomain attention),能够有效处理多物理场PDE问题,解决了传统神经算子在多物理场问题中遇到的一些关键难题。
CoDA-NO的创新点:
- 值域注意力机制:CoDA-NO通过在值域空间内对物理变量进行标记和自我监督学习,避免了传统方法的局限。通过扩展位置编码、注意力机制和正则化方法,CoDA-NO能够处理耦合的PDE问题,并能同时处理多个物理系统。
- 自监督预训练和少样本微调:CoDA-NO能够通过自监督学习对多个PDE系统进行预训练,学习不同PDE系统的表示,然后使用少量数据进行微调,从而解决数据不足的问题。
三、架构设计与方法
CoDA-NO架构基于Transformer,并对其进行了扩展,使其能够在函数空间内执行操作,从而处理多物理场PDE问题中的函数映射问题。
- 输入函数的表示: 输入的物理变量通过位置编码(variable-specific positional encoder, VSPE)和图神经算子(graph neural operator, GNO)进行处理。每个物理变量被视为一个函数,通过学习到的傅里叶系数表示相应的物理特征。
- 自注意力机制扩展: 在传统的Transformer架构中,注意力机制通过查询(query)、键(key)和值(value)来计算输出,而CoDA-NO将这一机制扩展到函数空间。
- 在CoDA-NO中,每个物理变量生成对应的键、查询和值函数,通过傅里叶神经算子(FNO)生成它们的表示。
- 通过计算查询与键之间的点积,得到的注意力权重应用到值函数上,从而得到输出函数。
- 正则化方法: CoDA-NO采用了一种在函数空间中的标准化方法,确保模型在不同物理系统下稳定工作。每个函数的标准化是基于其均值和标准差来进行的。
四、实验与结果
多物理场问题的应用:
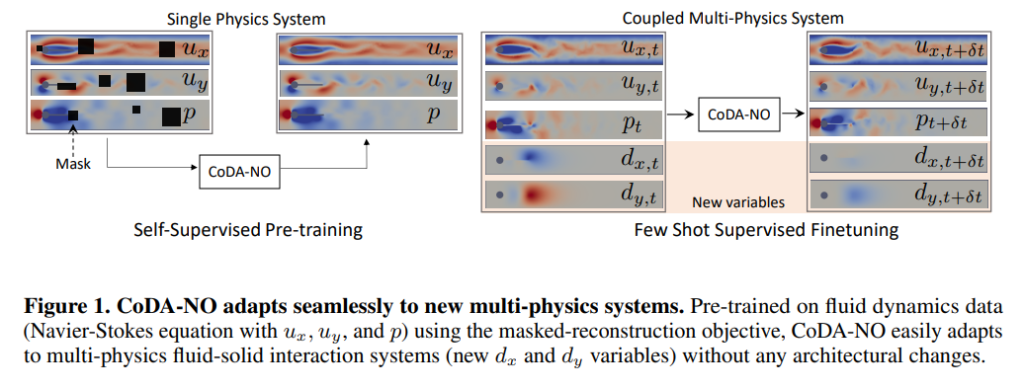
- 流体-结构相互作用问题: 在流体-结构耦合问题中,首先对Navier-Stokes方程进行预训练。通过少样本微调,模型能够适应弹性波方程的位移场。实验表明,CoDA-NO相较于现有方法提高了36.8%的准确度。
- Rayleigh-Bénard对流问题: CoDA-NO通过对Navier-Stokes方程的预训练,成功地适应了Rayleigh-Bénard对流问题。实验结果显示,在流体温度与速度耦合的情境下,CoDA-NO能显著提高预测精度,减少50%的误差。
与现有方法的比较:
- CoDA-NO在少样本学习中的表现优于其他方法。通过预训练,CoDA-NO能够迅速适应新的物理场系统,而不需要从头开始训练。
- 在实验中,CoDA-NO与现有的FNO、DeepONet等方法相比,在少量数据下的性能大幅提高,并且在多个物理系统上表现出色。
参数效率与计算效率:
- CoDA-NO在多个实验中表现出高效的参数利用率,比传统的FNO架构减少了最多43%的测试误差,且仅使用2%的参数。
- CoDA-NO能够处理不同分辨率的网格,适应多物理场系统的需求,避免了传统方法在处理不规则网格时的性能下降。
五、未来工作
- 结合物理启发的学习方法:进一步集成物理知识和模型约束,以提高模型在更复杂物理系统中的表现。
- 扩展应用领域:未来可以将CoDA-NO应用于更广泛的领域,如气候模拟、材料设计和生物医学工程等,以验证其在实际应用中的性能。
CoDA-NO on GitHub: https://github.com/neuraloperator/CoDA-NO