论文Understanding Transformer Reasoning Capabilities via Graph Algorithms《通过图算法理解 Transformer 的推理能力》主要探索了Transformer 在解决图推理任务时的理论与实践表现。Transformer能够高效解决许多复杂的图推理任务,尤其是在全局推理任务中表现优异。
论文作者为Clayton Sanford, Bahare Fatemi, Ethan Hall, Anton Tsitsulin, Mehran Kazemi, Jonathan Halcrow, Bryan Perozzi, Vahab Mirrokni,均来自Google。
一、背景
Transformer 自提出以来,已经成为深度学习领域的支柱性架构,广泛应用于自然语言处理(NLP)、计算机视觉(CV)及其他学科。然而,尽管 Transformer 在诸多应用场景中表现卓越,其推理能力在理论上的理解仍然有限,尤其是关于其能否在合理的参数规模下解决复杂算法问题。
- 为何研究图推理任务? 图是表达复杂关系和依赖的核心抽象形式,其应用场景涵盖社交网络分析、生物信息学、物流优化等。通过分析 Transformer 在图推理任务上的表现,可以深入理解其在处理带有复杂关系数据时的能力。
- 与图神经网络(Graph Neural Networks, GNN)对比: 图神经网络(如 GCN、GIN)是一类专门设计用于图数据的模型,能够高效捕获局部邻域信息。然而,GNN 在处理全局信息(如图连通性)时存在显著局限性,且其表达能力受限于 Weisfeiler-Lehman(WL)图同构测试。
二、研究动机
论文的主要目标是探索 Transformer 在解决图推理任务时的理论与实践表现,主要问题包括:
- 理论能力:Transformer 在多大深度、宽度或其他参数限制下能够解决哪些图推理问题?
- 任务分类:图推理任务如何根据计算复杂度分类?不同类别的任务对 Transformer 的要求如何?
- 与 GNN 比较:Transformer 在处理图数据时是否具有显著优势,尤其是在全局信息推理任务中?
三、主要贡献
论文的核心贡献包括:
- 提出了一个新的图推理任务复杂性层次结构:
- 将图推理任务划分为三类:
- 检索任务(Retrieval Tasks):如节点计数、边计数,这些任务只需简单查找或全局聚合。
- 可并行任务(Parallelizable Tasks):如连通性检测、循环检测,这些任务可以通过并行计算高效解决。
- 搜索任务(Search Tasks):如最短路径、图直径计算,需要更复杂的搜索算法。
- 提出了 Transformer 在不同参数规模下的适用性,如对数深度(LogDepth)、宽嵌入维度(LogDepthWide)等。
- 将图推理任务划分为三类:
- 理论证明:
- 对数深度 Transformer 足以高效解决可并行任务。
- 搜索任务需要更高的模型容量或更宽的嵌入维度。
- 检索任务可以由单层 Transformer 解决。
- 实验验证:
- 在 GraphQA 数据集上验证了理论结论,表明 Transformer 在全局推理任务中表现优于 GNN。
- 在小样本场景中,GNN 凭借其局部归纳偏置具有优势。
- 与 GNN 比较:
- Transformer 能模拟 GNN 的行为,同时在表达能力上超越 GNN,尤其是 2-WL 测试。
四、研究方法
一)图推理任务定义
论文重点研究了以下基础图推理任务:
- 检索任务:
- 节点计数:计算图中节点的总数。
- 边计数:计算图中边的总数。
- 边存在性:判断两节点之间是否存在边。
- 节点度:计算某节点的度数。
- 可并行任务:
- 连通性检测:判断两节点是否连通。
- 循环检测:判断图中是否存在循环。
- 二分图检测:判断图是否是二分图。
- 搜索任务:
- 最短路径:计算两节点之间的最短路径。
- 图直径:计算图中最长的最短路径。
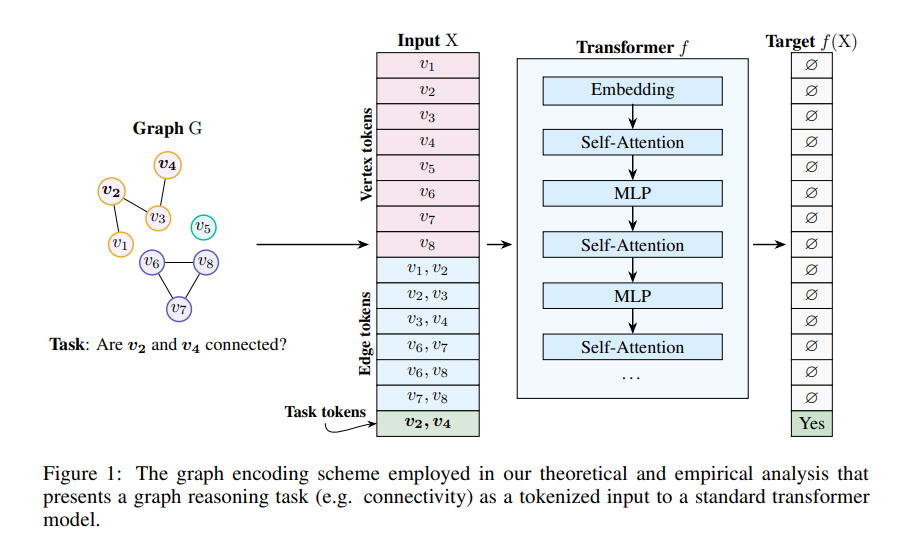
二)图数据的编码方式
论文采用了一种基于令牌化的图编码方式,将图的节点、边及任务信息转化为序列输入 Transformer。这种方法类似于 NLP 中的输入处理方式,使 Transformer 能够直接处理图数据。
三)Transformer 模型的理论假设
论文在理论上对 Transformer 模型的能力进行了建模,核心假设包括:
- 有限嵌入维度:模型的嵌入维度与图的大小呈次线性关系。
- 低秩自注意力矩阵:注意力机制限制了 Transformer 的信息交互能力。
- 暂停令牌(Pause Tokens):通过增加空白令牌扩展 Transformer 的计算能力。
五、理论分析
论文通过理论证明了 Transformer 对不同类别任务的适用性:
- 检索任务:
- 单层 Transformer 足以解决此类任务,因为它们只需简单的聚合或查找操作。
- 可并行任务:
- Transformer 可以高效并行模拟这些任务,如连通性检测可以通过对数深度 Transformer 完成。
- 搜索任务:
- 搜索任务需要更大的模型容量,尤其是更宽的嵌入维度或更深的网络。
论文借助大规模并行计算(MPC)模型,将 Transformer 的能力与经典算法的并行实现进行类比。通过证明 Transformer 可以高效模拟 MPC 协议,验证了其在图推理任务中的理论性能。
六、实验设计
论文使用 GraphQA 数据集对理论结果进行了实验验证,实验包含以下内容:
- 模型对比:
- 小型 Transformer(60M 参数)。
- 大型预训练 Transformer(T5,11B 参数)。
- 经典 GNN 模型(GCN、MPNN、GIN)。
- 任务范围:
- 覆盖检索任务、可并行任务及搜索任务。
- 评估指标:
- 准确率(Accuracy)。
- 训练样本数量的影响。
实验结果:
- Transformer 在全局推理任务中的表现:
- 在连通性检测任务中,小型 Transformer 随着训练样本数量增加,其准确率迅速提高,最终超过 GNN。
- 在最短路径任务中,预训练的大型 Transformer 表现优于所有 GNN。
- GNN 在本地推理任务中的优势:
- 在节点度数计算和循环检测任务中,GNN 在小样本场景下优于 Transformer,归因于其局部归纳偏置。
- 提示方法的局限性:
- 提示方法(如零样本、少样本)在解决图推理任务时性能显著低于专门训练的 Transformer。
七、结论与未来方向
一)结论
- Transformer 能够高效解决许多复杂的图推理任务,尤其是在全局推理任务中表现优异。
- 理论与实验结果一致,证明了对数深度 Transformer 的表达能力。
- GNN 在小样本任务中有优势,但在大规模数据场景下难以与 Transformer 竞争。
二)未来研究方向
- 扩展任务范围:探索更多类型的算法问题及其对 Transformer 表达能力的要求。
- 模型优化:研究具有有限 MLP 单元的 Transformer 在实际任务中的表现。
- 学习能力分析:进一步分析 Transformer 在小样本学习任务中的适用性。