利用混合整数线性优化（Mixed-Integer Linear Programming, MILP）改进 PINNs初始权重，提高训练收敛速度和精度

物理信息神经网络（Physics-Informed Neural Networks，PINNs）是一种新兴的深度学习方法，它结合了前馈神经网络（Feedforward Neural Network，FNN）与用常微分方程（ODE）或偏微分方程（PDE）表示的系统先验知识。这种方法在流体物理、动力系统、能源系统、热扩散等多个科学领域得到了广泛应用。PINNs 的优势在于能够结合物理规律进行建模，使其能够应用于求解复杂的物理问题。然而，PINNs 仍然存在训练收敛速度较慢的问题，尤其是在涉及现实复杂系统的情况下。

在 PINNs 的标准训练过程中，网络权重的初始化通常采用随机分布，如 Glorot（Xavier）初始化方法。然而，这种随机初始化可能导致训练过程中的收敛瓶颈，使得网络难以有效收敛甚至无法收敛。因此，研究者们开始探索更优的初始化方法，以提高 PINNs 的收敛速度和稳定性。

论文MILP initialization for solving parabolic PDEs with PINNs提出了一种利用混合整数线性规划（Mixed-Integer Linear Programming, MILP）优化的方法来改进 PINNs 的初始权重。作者研究了两种不同的优化策略作为网络训练的预训练步骤：（1）仅包含边界条件的优化；（2）结合物理约束的优化。优化主要针对 PINNs 的第一层权重，而其他层仍采用随机初始化。论文采用热扩散方程作为测试案例，模拟电力变压器的温度分布，并分析了不同初始化策略对 PINNs 训练收敛速度的影响。

论文作者为Sirui Li, Federica Bragone, Matthieu Barreau, Kateryna Morozovska，来自KTH Royal Institute of Technology。

一、论文方法

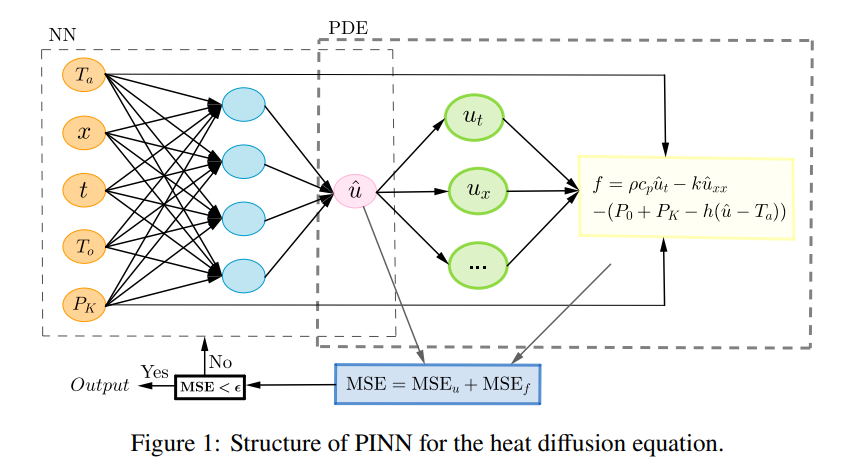
1. 物理信息神经网络（PINNs）

PINNs 通过在神经网络的损失函数中显式地融入物理方程，使网络能够学习系统的动力学特性。本文使用了一个具有单个隐藏层的 PINN，其数学表示如下：û(X)=W₂σ(W₁X+b₁)+b₂，其中：

σ为隐藏层的激活函数（如 tanh⁡）
W₁,W₂为权重矩阵
b₁,b₂为偏置
X为输入向量
û为网络输出

PINNs 的损失函数由边界条件误差（MSE_u）和方程残差误差（MSE_f）组成：

L=λ_uMSE(û(X_u),u)+λ_fMSE(f[û](X_f),0)

其中：

X_u和u分别表示边界点的输入与目标输出
X_f为方程求解点（collocation points），PINNs 在这些点上满足偏微分方程

2. 热扩散方程

本文的实验测试使用 一维热扩散方程 来模拟电力变压器的温度分布：

ρc_pu_t=ku_xx+q

其中：

ρ为密度
c_p为比热容
k为热导率
q为热源项，定义为：

q=P₀+P_K(x,t)−h(u−T_a)

其中：P₀为空载损耗；P_K(x,t)为负载损耗，依赖于负载因子 K(t)；hhh 为对流换热系数；T_a为环境温度；

变压器的温度边界条件为：

u(x₀,t)=Ta, u(x_end,t)=T_o

其中 T_o为变压器顶部油温。

3. 优化模型

为了解决 PINNs 随机初始化导致的训练瓶颈问题，本文采用 混合整数线性优化（MILP） 来改进权重初始化。主要优化目标是：

边界预训练（Boundary Pre-training）： 仅在边界点上拟合温度。
全域预训练（Full Pre-training）： 在边界点和物理方程残差点上拟合温度。

MILP 通过将激活函数 tanh⁡(x)近似为 饱和函数（Saturation function） 来简化优化问题：

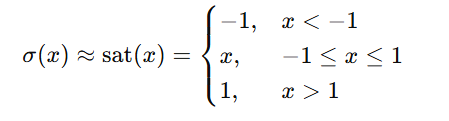
利用该近似方法，MILP 通过求解线性规划问题来确定最优的初始权重，并使用该权重进行 PINNs 训练。

三、结果与讨论

1. 预训练初始化效果

采用 MILP 预训练的初始权重在温度预测范围上更接近真实解（由 COMSOL 模拟提供）。
边界预训练和全域预训练相比随机初始化的 PINN在初始预测时具有更合理的温度分布。

2. 收敛速度分析

边界预训练 PINN 的收敛速度最快：
- 32 个隐藏神经元时，边界预训练的 MSE 下降至 0.0184，相比普通 PINN（0.0579）有显著提升。
- 60 个隐藏神经元时，边界预训练的 MSE 下降至 0.0059，而普通 PINN 为 0.0395。
全域预训练的收敛速度未显著提升：
- 由于物理损失函数的非线性逼近存在误差，全域预训练的效果反而不如边界预训练。
训练时间比较：
- 边界预训练 PINN 训练时间显著缩短（约 20 分钟）。
- 普通 PINN 和全域预训练 PINN 需要约 30-35 分钟。

3. 预测精度评估

经过 10000 轮训练后，所有 PINN 模型都能准确预测温度分布，但边界预训练 PINN 仍然在误差上更小。
不同时刻的温度分布曲线与 COMSOL 结果一致，表明优化后的 PINN 训练能够有效捕捉热扩散过程。

四、结论

本文研究了使用混合整数线性优化（MILP）来改进 PINNs 的初始权重，以提高训练收敛速度和精度。主要结论如下：

边界预训练比随机初始化显著提升收敛速度和预测精度。
全域预训练未能明显改善 PINN 训练，可能受到非线性近似误差的影响。
在电力变压器热扩散问题上，优化后的 PINN 训练时间缩短约 40%，收敛误差降低 3-5 倍。

未来研究方向包括：

优化激活函数近似方法，提升物理约束预训练的精度。
将该方法推广至更复杂的 PDE 问题，如湍流模拟和流固耦合问题。