论文The Geometry of Concepts: Sparse Autoencoder Feature Structure(《概念几何:稀疏自编码器特征结构》)分析了稀疏自编码器(SAE)在激活空间中表示概念的特征点云结构,从微观、中观和宏观三个层次探讨了其几何特性。
论文作者为Yuxiao Li, Eric J. Michaud, David D. Baek, Joshua Engels, Xiaoqing Sun, Max Tegmark,均来自麻省理工(MIT)。
如下为论文概要内容:
1. 引言与研究背景
近年来,稀疏自编码器(Sparse Autoencoder, SAE)在分析大型语言模型的激活空间方面取得了重要进展。这些自编码器通过无监督方式从语言模型的激活空间中提取出一系列被称为“特征”的点云,这些特征可以代表不同的语义概念。例如,通过对语言模型的特征进行研究,我们能够更好地理解模型如何内部表示抽象概念。论文引用了诸如Huben et al.(2023)和Bricken et al.(2023)等人的研究,表明这些特征具有显著的几何结构。特别是,这些特征点云通过可视化工具(如UMAP)展示了其分布倾向于形成特定群体,而非像以往认为的那样接近于正交。
这篇论文的目标是通过深入分析稀疏自编码器所生成的高维特征,揭示其在概念空间中的几何结构。具体来说,论文将这些特征点云的几何结构分为三个尺度进行研究:微观的“原子”尺度、中观的“脑”尺度以及宏观的“星系”尺度,每一个层次代表了不同的研究视角和挑战。
2. 原子尺度的晶体结构
在微观层次,论文试图找到在概念空间中表现出“晶体”特征的几何结构。所谓晶体结构,类似于平行四边形或梯形,这些结构反映了特定概念之间的语义关系。例如,经典的语义关系“man:woman::king:queen”可以被表示为两个相似的向量差值形成的平行四边形,其中“man”与“woman”之间的向量差值应与“king”与“queen”之间的向量差值相似。
为了识别这种结构,作者计算了特征点云中所有成对向量的差值,然后对这些差值进行聚类。通过这种方法,作者希望找到每一个功能向量所对应的聚类,任何在同一个聚类中的向量对应的向量差应该形成梯形或平行四边形。然而,最初的实验结果显示,大多数的差值向量在未进行处理时只是噪声。这种噪声的来源被认为是存在许多“干扰特征”,例如单词的长度,这些干扰特征并不直接与语义相关,却对差值向量的质量造成了显著影响。
为了解决这一问题,作者使用了线性判别分析(Linear Discriminant Analysis, LDA)来去除这些干扰特征。LDA的主要作用是通过最大化信号与噪声之间的方差比,找到对概念表示有意义的维度,从而使得语义特征更清晰地显现出来。在去除干扰特征后,作者观察到平行四边形和梯形结构的质量显著提高,验证了干扰特征对晶体结构的影响。
3. 脑尺度的中观模块化结构
在中观层次,作者探讨了稀疏自编码器特征的“脑叶”结构,这些结构类似于生物大脑中的功能分区。例如,人类大脑中不同区域负责不同的功能,如布罗卡区负责语言生成,听觉皮层负责声音处理等。作者假设,稀疏自编码器所学习到的特征点云也会存在类似的功能模块化结构。
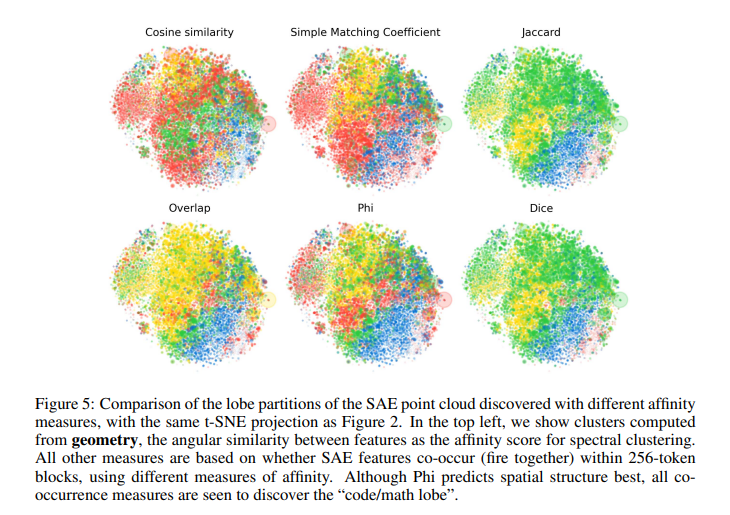
为了验证这一假设,作者首先通过处理大量文档,计算特征在文档中的共现直方图。具体来说,作者使用了“Gemma-2-2b”自编码器对来自The Pile(一个包含多种文档类型的数据集)中的文档进行处理,记录在每个256个token的块中哪些特征被激活。作者接着基于这些共现数据计算特征之间的亲和度,使用了包括简单匹配系数、Jaccard相似度、Dice系数、重叠系数和Phi系数等多种方法对特征点云进行光谱聚类,以识别特征之间的功能性“脑叶”结构。
实验结果显示,这些功能性“脑叶”在几何空间中表现出显著的模块化特征。例如,数学和代码相关的特征倾向于聚集在一起,形成一个独立的模块,而与一般英语文本相关的特征则形成另一个模块。通过对比功能性聚类和基于几何相似度的聚类,作者发现这两者之间具有较高的互信息,这表明功能性模块与几何空间中的特征分布存在紧密联系。此外,作者通过训练逻辑回归模型来预测功能模块标签,进一步验证了特征的模块化结构,实验结果表明这种模块化的空间分布是显著的。
4. 星系尺度的大尺度点云结构
在宏观层次,作者研究了特征点云的整体结构,重点考察其形状和聚类特性。为了分析特征点云的形状,作者首先计算了点云协方差矩阵的特征值,并发现这些特征值遵循幂律分布,而不是像各向同性的高斯分布那样具有一致的特征值。这表明特征点云的形状更接近于“分形黄瓜”(fractal cucumber),即在连续的维度中其宽度呈现幂律递减。这种现象在中间层尤其明显,暗示模型在中间层可能执行了一种信息压缩的功能,将信息浓缩到更少的主成分中,从而实现高层次概念的有效表示。
为了进一步验证特征点云的聚类特性,作者采用了k近邻方法估计了点云的熵值,并计算了聚类熵(即与高斯分布相比的熵值减少量)。结果显示,中间层的特征点云具有最低的聚类熵,这意味着这些层的特征更加集中、紧密。这种现象可能是由于中间层需要更有效地表示语义信息,而模型的早期和后期层次更多地分散了这些特征,以捕获不同层次的信息。
5. 结论与实际意义
通过对稀疏自编码器特征点云的三层结构分析,论文得出以下主要结论:
- 原子尺度(晶体结构):概念空间中存在类似于“晶体”的几何结构,如平行四边形或梯形,反映了特定的语义关系。在去除干扰特征后,这些结构更加明显。
- 脑尺度(模块化结构):稀疏自编码器的特征点云表现出功能性模块化,类似于生物大脑中的不同功能区。例如,数学和代码特征形成了独立的功能模块,这种模块化结构在几何上具有显著性。
- 星系尺度(大尺度点云结构):特征点云整体上表现出幂律分布,这表明中间层执行了信息压缩,将语义信息浓缩到更少的主成分中。此外,特征点云在中间层的聚类熵最低,表明这些特征更加集中和紧密。
这些发现为理解稀疏自编码器特征和大型语言模型的内部机制提供了基础。作者希望这些研究能够成为进一步探索语言模型工作原理的基础,从而揭示这些模型在处理和表示概念方面的独特特性。
6. 未来工作与应用
未来的研究可以在以下几个方面进行深入探索:
- 干扰特征的进一步研究:目前的研究通过LDA去除了一些干扰特征,但如何更全面和自动化地识别这些干扰特征仍是一个开放问题。未来可以尝试通过其他无监督或半监督方法进一步改进特征提取的质量。
- 功能性模块的演变:作者发现不同功能模块在模型的不同层次具有不同的表现,未来可以深入研究这些模块如何随着训练进程和层次而演变,这对于理解模型内部的表示学习过程具有重要意义。
- 幂律分布的起源:幂律分布在特征点云中的出现是一个有趣的现象,未来研究可以尝试解释为什么这种结构在中间层最为显著,以及它与模型的性能、泛化能力之间的关系。