论文rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking提出了rStar-Math,以证明小型语言模型(Small Language Models,SLMs)能够与OpenAI o1的数学推理能力相媲美,甚至超越,而无需依赖更高级模型的蒸馏过程。
论文作者为Xinyu Guan, Li Lyna Zhang, Yifei Liu, Ning Shang, Youran Sun, Yi Zhu, Fan Yang, Mao Yang,均来自Microsoft Research Asia。
一、引言
本文提出了rStar-Math,一个专注于提升小型语言模型(Small Language Models, SLMs)在数学推理任务中表现的系统。相比依赖于大型语言模型(Large Language Models, LLMs)进行知识蒸馏的传统方法,rStar-Math完全通过自我进化的方式,不依赖教师模型,从零开始发展出强大的数学推理能力。其核心思想是利用系统2式推理(System 2 reasoning),即一种类似人类深度思考的逐步推理方式,从而超越当前大模型在数学问题上的表现。
具体来说,rStar-Math通过以下三大技术创新,实现了小模型在数学推理能力上的重大突破:
- 代码增强的逐步链式思维数据合成方法:通过蒙特卡洛树搜索(Monte Carlo Tree Search, MCTS)生成逐步验证的推理路径,确保中间每一步推理均正确无误,并通过代码执行进行验证。
- 过程偏好模型(Process Preference Model, PPM):改进了奖励模型训练方法,不再依赖传统的逐步打分机制,而是通过偏好对(preference pairs)的方式,更高效地优化推理步骤的评价。
- 四轮自我进化策略:在无任何预训练数据的情况下,通过自我生成、优化和迭代,逐步提升SLM的推理能力,解决更复杂的数学问题。
实验结果表明,rStar-Math在多个数学基准上达到了或超越了最先进模型的水平。例如,在MATH基准上,rStar-Math将Qwen2.5-Math-7B模型的准确率从58.8%提高到90.0%;在AIME(美国数学奥林匹克邀请赛)测试中,能够解决53.3%的问题,相当于进入全美高中数学竞赛学生中的前20%。
二、背景与动机
随着大语言模型的快速发展,其在数学推理任务中的表现受到了广泛关注。然而,目前主流方法仍面临以下三个主要挑战:
- 高质量数学推理数据稀缺
数学推理需要模型生成不仅正确的最终答案,还需要完整且准确的推理路径。然而,现有数据集大多依赖人类标注或通过大型模型(如GPT-4)进行蒸馏生成。这种方法不仅成本高昂,且生成的数据往往受到教师模型能力的限制,尤其在复杂问题上难以取得突破。 - 中间推理路径的错误累积问题
在数学推理任务中,正确的最终答案并不意味着推理路径完全正确。中间步骤中任何错误都会显著降低数据质量,并影响模型的训练效果。现有方法往往难以区分推理路径中存在的细微错误。 - 奖励模型的训练瓶颈
高效的数学推理需要依赖于能够精确评估每一步推理的奖励模型。然而,目前的奖励模型训练依赖大量人工标注,难以大规模扩展。此外,自动化的标注方法(如基于结果的打分)往往过于粗糙,无法提供足够精细的反馈信号。
针对此,rStar-Math提出了一种全新的思路:通过小型模型自我生成高质量数据,并结合逐步验证和偏好建模的方法,实现模型推理能力的自我迭代优化。这不仅摆脱了对大型模型的依赖,也为小模型在复杂任务上的应用提供了新的可能。
三、方法论
rStar-Math的方法论可以分为以下三个关键部分:
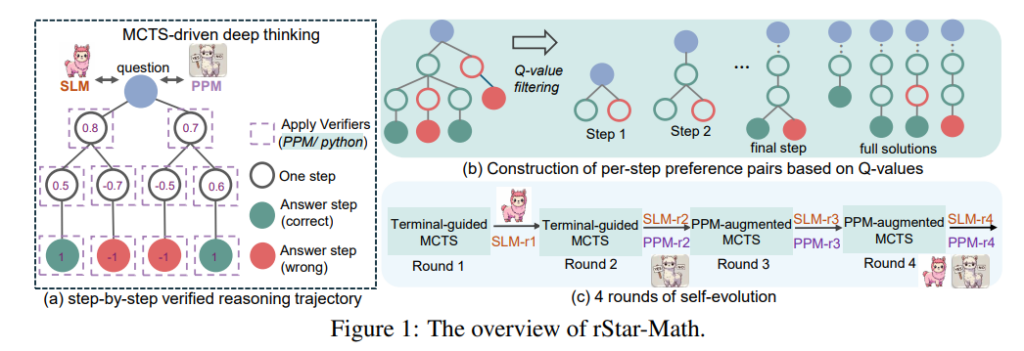
1. 基于MCTS的逐步验证推理路径生成
MCTS是一种适合解决逐步决策问题的搜索算法,被广泛应用于棋类游戏中的智能决策。本文将其引入数学推理任务,通过以下步骤生成高质量的逐步验证推理路径:
- 逐步生成与代码验证:在每一步推理中,模型同时生成自然语言描述和对应的Python代码。生成的代码需通过执行验证,只有代码能够正确执行的路径才被保留。
- Q值标注与评分:对于每个中间步骤,通过MCTS的回溯机制,赋予其基于最终结果的贡献值(Q值)。通过多次搜索迭代,确保Q值标注的准确性和可靠性。
这部分方法有效解决了传统推理路径生成中常见的错误累积问题。
2. 过程偏好模型(PPM)
传统奖励模型的训练往往依赖精确的逐步评分,这不仅成本高昂,且难以确保一致性。rStar-Math通过构造偏好对,替代了传统的逐步打分机制:
- 偏好对的构造:在每个步骤中,从MCTS生成的路径中选择两个高评分的正样本和两个低评分的负样本,形成正负偏好对。
- 基于排序损失的优化:通过对偏好对的排序损失函数进行优化,训练过程偏好模型,使其能够更准确地预测每一步推理的得分。
这种方法避免了传统逐步评分中的噪声问题,同时显著提升了模型对关键推理步骤的捕捉能力。
3. 四轮自我进化策略
rStar-Math通过四轮自我迭代的方式,逐步提升SLM的推理能力:
- 第一轮:初始化强基线模型
使用外部模型(如DeepSeek-Coder)生成初始训练数据,训练第一代SLM和初步的PPM。 - 第二轮:优化奖励模型
通过更精确的Q值标注,生成高质量推理路径,用于训练更可靠的PPM。 - 第三轮:基于PPM的优化搜索
使用PPM改进MCTS搜索质量,生成更多覆盖复杂问题的数据。 - 第四轮:解决高难度问题
针对未解决的复杂问题,通过增加搜索迭代次数和随机性,进一步提升覆盖率。
最终,这种逐步进化的策略将SLM的数学推理能力提升至最先进水平。
四、实验与结果分析
实验在多个数学基准上验证了rStar-Math的有效性,涵盖基础数学(如MATH)、竞赛数学(如AIME、奥赛)以及大学数学等多个领域。
1. 基准测试结果
rStar-Math在多个任务上的表现显著优于现有方法。例如:
- 在MATH基准上,Qwen2.5-Math-7B模型的准确率从58.8%提升至90.0%,超过了OpenAI o1-preview。
- 在AIME测试中,rStar-Math解决了53.3%的问题,表现优于大多数开源模型。
- 在奥赛级别和大学数学任务上,rStar-Math同样展现了强大的推理能力。
2. 逐步验证路径的有效性
相比于传统的数据合成方法(如GPT-4蒸馏数据),逐步验证路径显著提升了模型的训练效果。在同样的训练条件下,基于验证路径的训练数据使模型的推理准确率提高了5%以上。
3. PPM的作用
实验表明,PPM不仅能有效提升复杂问题的推理精度,还能自动识别关键的定理应用步骤(如费马小定理、勾股定理等),为模型提供明确的推理指导。
五、关键发现
- 自我反思能力的涌现
实验发现,rStar-Math在推理过程中会主动识别错误路径并调整策略,这种自我反思能力源于System 2推理的逐步验证机制。 - 定理应用的偏好识别
PPM能够识别出推理过程中关键的定理应用步骤,为复杂问题的解决提供指导。 - 小模型的潜力
通过自我生成和优化,小模型可以在不依赖大模型蒸馏的情况下,达到甚至超越大模型的性能。
六、总结与展望
rStar-Math通过系统2式推理方法,展现了小模型在数学推理任务中的巨大潜力。未来工作可进一步探索更多样化的数据集和其他领域(如代码推理、通用逻辑推理)的应用。