论文Physics-constrained coupled neural differential equations for one dimensional blood flow modeling提出了PCNDE框架(Physics-constrained coupled neural differential equations,物理约束神经微分方程框架),该框架在提高1D血流模型精度的同时,保持了较高计算效率,成功弥补了传统1D FEM模型在复杂血流情况下的不足。通过空间域的重构和傅里叶周期性约束,PCNDE在精度和稳定性方面均表现出了较佳性能。
论文作者为Hunor Csala, Arvind Mohan, Daniel Livescu, Amirhossein Arzani,来自University of Utah和Los Alamos National Laboratory。
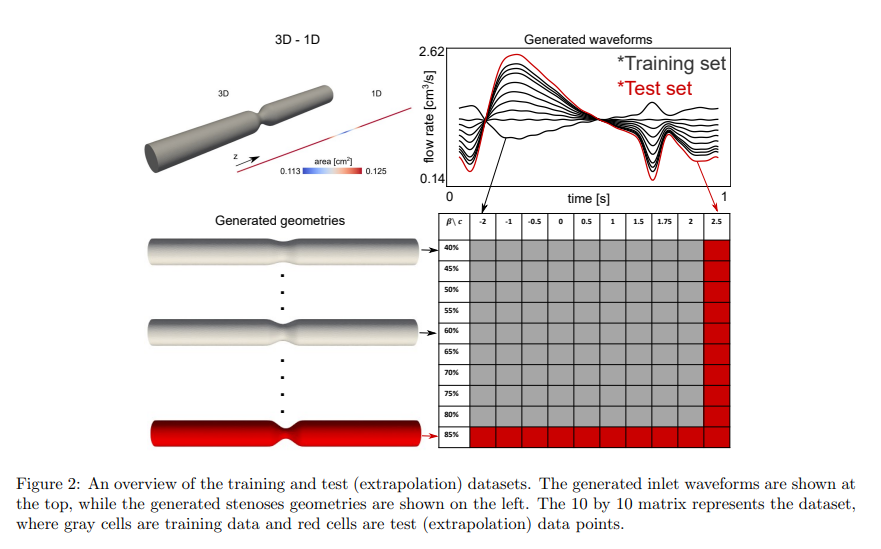
一、研究背景与目标
心血管疾病是全球范围内主要的死亡原因之一,理解血液流动的动力学特性对于临床诊断与治疗至关重要。传统的血流动力学建模方法,包括详细的三维流体-结构耦合(FSI)模型,能够提供准确的血流细节,但计算代价极高,限制了其在临床中的广泛应用。为了提高计算效率并在保持一定准确性的同时使模型适用于实时分析,简化模型成为一个必要方向。
1D血流模型通过对Navier-Stokes方程进行截面平均化简化了复杂的三维方程系统,通常用于模拟血管内的血液流动。尽管1D模型计算上更加高效,但其精度相较于3D模型较低,尤其在复杂几何结构(如动脉狭窄)下,传统的有限元方法(FEM)1D模型往往无法有效捕捉这些复杂流动情况。为了解决这一问题,本文提出了一种新型的物理约束神经微分方程(PCNDE)框架,旨在通过机器学习方法提高1D血流模型的精度,同时保持其计算效率。该方法结合了物理模型与数据驱动方法,创新性地将血流动力学的物理约束与神经网络相结合,从而在计算速度和准确度之间实现平衡。
二、方法与框架
1. 物理模型与数据生成
传统的1D血流模型通过对3D Navier-Stokes方程进行截面平均简化,得到如下两条主要的方程:
- 连续性方程:描述了血流速率(Q)与血管截面积(S)之间的关系:
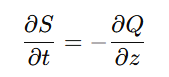
- 动量方程:通过动量守恒计算压力变化:
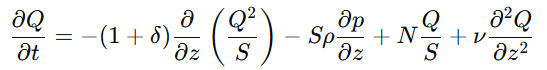
其中,Q是流量,S是血管截面积,ρ是血液密度,ν是血液的运动粘度,p是压力,t是时间,z是沿血管轴向的坐标。
为训练PCNDE模型,本文使用SimVascular进行100个不同3D FSI模拟,涵盖了10种不同的动脉狭窄比例(β)和10种不同的流入边界条件。通过这些模拟数据生成训练集,为后续的PCNDE模型提供基础数据。
2. PCNDE框架
PCNDE框架的核心创新在于将传统的时间域神经微分方程(NDE)重新表述为空间域的神经微分方程。具体来说,本文通过以下步骤实现了PCNDE的计算框架:
- 空间域动量方程:通过神经网络拟合动量方程中的未知项,并将方程转换为空间形式进行求解,解决了传统时间域方法中衍生不平滑的问题。
- 傅里叶级数约束:为确保血管截面积的时间周期性,使用傅里叶级数对面积的预测值进行修正。这样可以强制执行血流周期的周期性特征。
- 压力模型:压力方程采用两阶段模型:第一阶段使用神经网络拟合压力的时间变化,第二阶段则采用解析模型捕捉空间上的压力变化。
这一框架的目标是通过结合物理知识和数据驱动的学习,提高1D模型的精度,同时保持1D模型在计算上的优势。
三、实验结果与分析
1. 流量、截面积和压力的预测结果
PCNDE模型在流量、截面积和压力预测方面表现出显著优于传统1D FEM模型的精度:
- 流量预测:PCNDE模型在测试集上的误差相比传统1D FEM小3至5倍,能较好地捕捉血流的时间和空间变化。
- 截面积预测:PCNDE能够较好地预测血管截面积的变化,尤其是在动脉狭窄处,但在周期的开始和结束阶段有一定的过度估计。
- 压力预测:PCNDE能够更准确地模拟压力变化,尤其是在较高压力区,传统1D FEM模型在此表现不佳。
此外,PCNDE模型的预测结果与3D模型的平均数据相比,最大误差不超过1.2%,表明其在处理真实世界中复杂的血流模型时具有较高的鲁棒性。
2. 稳定性与鲁棒性分析
在训练过程中,PCNDE模型展示了良好的稳定性,尤其是在通过空间域的转换处理动量方程后,模型在耦合稳定性和光滑性方面显著改进。尽管初期的时间域模型在流速的空间导数上存在不平滑问题,但这种问题通过空间域的转换得到了有效解决。模型对输入数据的噪声也表现出了较强的鲁棒性,通过在输入边界条件中添加噪声,PCNDE的预测结果仍然能够保持与真实数据相似的精度。
3. 误差分析
PCNDE模型在测试集中的相对误差明显低于1D FEM模型。尤其是在流量和压力预测方面,PCNDE模型的误差均低于1%,而传统的1D FEM模型则存在更大误差。图表中的误差分布显示,最大误差主要集中在动脉狭窄区域和特殊的流入波形条件下,这表明PCNDE模型能够在这些复杂情况下提供更精确的预测。
四、讨论与未来展望
1. 方法的优势
PCNDE框架结合了物理约束和数据驱动方法,成功地弥补了传统1D模型在精度上的不足。通过采用傅里叶级数强制时间周期性,PCNDE不仅提升了流量和压力的预测准确性,还在计算效率上保持了1D模型的优势。该方法特别适用于需要快速预测的临床应用,能够在不牺牲精度的情况下提供实时模拟。
2. 当前挑战与不足
尽管PCNDE在大多数测试情况下表现良好,但仍面临一些挑战:
- 复杂几何结构:模型主要针对理想化的动脉几何,在处理具有更复杂弯曲或多分支结构时,可能需要进一步调整和优化。
- 多尺度建模问题:血流动力学是一个典型的多尺度问题,时间和空间的变化幅度相差悬殊。在处理如动脉狭窄等问题时,如何在空间和时间尺度上更精确地拟合仍是一个挑战。
3. 未来发展方向
- 患者特异性几何结构的处理:未来的研究将进一步扩展PCNDE框架,考虑患者个体的复杂动脉几何和变形,进而提高其在临床中的实际应用价值。
- 更大规模的训练数据集:为了提高模型的泛化能力,未来需要构建一个涵盖更多复杂几何和不同边界条件的大规模训练数据集。
- 与自动化检测工具结合:结合自动化工具(如基于图形的学习方法)来更有效地处理多分支动脉的建模问题,提升模型的适应能力和普适性。
对于是否采用了物理信息神经网络PINNs(Physics-Informed Neural Networks),论文作者Hunor Csala有如下解释:
我们使用了普适微分方程(Rackauckas等,2020)框架,将神经网络和其他可优化的向量作为微分方程中的项。PDE(偏微分方程)通过经典的数值方法求解,只是采用可微的方式以便允许反向传播。在损失函数中,物理约束并不像物理信息神经网络(PINN)中那样被强制执行;损失仅仅是预测与数据之间的均方误差(MSE)。此外,神经网络的输入是感兴趣的变量(例如流量),而不是空间和时间。因此,这种方法与PINN有很大的不同。